In the circuit shown here, the point \(C\) is kept connected to point a till the current flowing through the circuit becomes constant. Afterward, suddenly, point \(C\) is disconnected from point \(A\) and connected to point \(B\) at time \(t=0\). The ratio of the voltage across resistance and the inductor at \(t=\frac{L}{R}\) will be equal to:

1. \(1\)
2. \(-1\)
3. \(\dfrac{1-e}{e}\)
4. \(\dfrac{e}{1-e}\)
1. \(1.67~\text{H}\)
2. \(6~\text{H}\)
3. \(3~\text{H}\)
4. \(0.67~\text{H}\)
In a coil of resistance \(100~\Omega\), a current is induced by changing the magnetic flux through it (as shown in the graph). The magnitude of the change in the flux through the coil is:

1. \(200~\text{Wb}\)
2. \(225~\text{Wb}\)
3. \(250~\text{Wb}\)
4. \(275~\text{Wb}\)
1. \(\frac{\pi \mu_{{o}}{I}_{{o}} {b}^2\omega \cos (\omega {t})}{{a}} \)
2. \(\frac{\pi \mu_{{o}}{I}_{{o}} {a}^2\omega \sin (\omega {t})}{{2b}} \)
3. \(\frac{\pi \mu_{{o}}{I}_{{o}} {a}^2\omega \sin (\omega {t})}{{b}} \)
4. \(\frac{\pi \mu_{{o}}{I}_{{o}} {a}^2\omega \cos (\omega {t})}{{2b}} \)
1. \(\frac{3}{2}nBA\omega\)
2. \(3nBA\omega\)
3. \(nBA\omega\)
4. \(\frac{1}{2}nBA\omega\)
A \(20\) Henry inductor and coil is connected to a \(10~\Omega\) resistance in series as shown in the figure. The time at which the rated of dissipation of energy (Joule’s heat) across the resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
1. \( \frac{1}{2} \ln 2 \)
2. \( \ln 2 \)
3. \( 2 \ln 2 \)
4. \( \frac{2}{\ln 2}\)
The total number of turns and the cross-sectional area of a solenoid are fixed. However, its length \(L\) is varied by adjusting the separation between the windings. The inductance of the solenoid will be proportional to:
| 1. | \(L\) | 2. | \(L^2\) |
| 3. | \(\dfrac{1}{L^2}\) | 4. | \(\dfrac{1}{L}\) |
Two coil '\(P\)' and '\(Q\)' are separated by some distance. When a current of \(3~\text{A}\) flows through coil '\(P\)' a magnetic flux of \(10^{-3}~\text{Wb}\) passes through '\(Q\)'. No current is passed through '\(Q\)'. When no current passes through '\(P\)' and a current of \(2~\text{A}\) passes through '\(Q\)', the flux through '\(P\)' is:
1. \( 6.67 \times 10^{-3} ~\text{Wb} \)
2. \( 3.67 \times 10^{-4} ~\text{Wb} \)
3. \( 6.67 \times 10^{-4}~\text{Wb} \)
4. \( 3.67 \times 10^{-3} ~\text{Wb} \)
A very long solenoid of radius \(R\) is carrying current \(I(t)=k t e^{-\alpha t}(k>0),\) as a function of time \((t\geq0).\) Counter clockwise current is taken to be positive. A circular conducting coil of radius \(2R\) is placed in the equatorial plane of the solenoid and concentric with the solenoid. The current induced in the outer coil is correctly depicted, as a function of time, by:
| 1. | 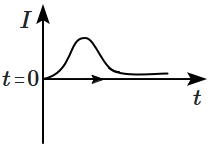 |
2. |  |
| 3. |  |
4. |  |
A coil of self inductance \(10~\text{mH}\) and resistance \(0.1~ \Omega\) is connected through a switch to a battery of internal resistance \(0.9~ \Omega\). After the switch is closed, the time taken for the current to attain \(80\%\) of the saturation value is: [take \(\ln 5=1.6\)]
1. \(0.324~\text{s}\)
2. \(0.002~\text{s}\)
3. \(0.103~\text{s}\)
4. \(0.016~\text{s}\)







