1. \(0.02~\text{km}\)
2. \(0.03~\text{km}\)
3. \(0.05~\text{km}\)
4. \(0.04~\text{km}\)
A block starts moving up an inclined plane of inclination \(30^\circ\) with an initial velocity of \(v_0\). It comes back to its initial position with velocity \(\frac{v_0}{2}\). The value of the coefficient of kinetic friction between the block and the inclined plane is close to \(\frac{I}{1000}\). The nearest integer to \(I\) is:
1. \(210\)
2. \(346\)
3. \(972\)
4. \(100\)
A boy pushes a box of mass \(2\) kg with a force \(\vec{F}=(20\hat{i}+10 \hat{j})~\text{N}\) on a frictionless surface. If the box was initially at rest, then the displacement along the \(\mathrm{x}\)-axis after \(10\) s is:
1. \(100\) m
2. \(300\) m
3. \(500\) m
4. \(700\) m
As shown in the figure, a block of mass \(\sqrt{3}\) kg is kept on a horizontal rough surface of coefficient of friction \(\dfrac{1}{3\sqrt{3}}\). The critical force to be applied on the vertical surface as shown at an angle \(60^\circ\) with horizontal such that it does not move, will be \(3x\). The value of \(x\) will be:
\((g=10 \mathrm{~m} / \mathrm{s}^2 ; \sin 60^{\circ}=\frac{\sqrt{3}}{2} ; \cos 60^{\circ}=\frac{1}{2})\)
1. \(1.23\)
2. \(4.5\)
3. \(3.33\)
4. \(9.24\)

1. \(5\)
2. \(10\)
3. \(14\)
4. \(12\)
1. When the elevator moves upward with constant acceleration.
2. When the elevator moves downward with constant acceleration.
3. When the elevator moves upward with uniform velocity.
4. When the elevator moves downward with uniform velocity.
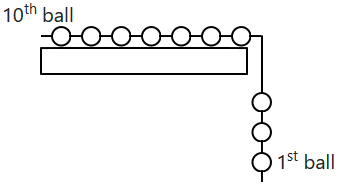
1. 24 N
2. 28 N
3. 32 N
4. 36 N
(Neglect the mass of the string and friction of the block (bigger mass) with ice slab.) (Given g = acceleration due to gravity)

1. 6
2. 3
3. 9
4. 2

1. 3
2. 6
3. 5
4. 4
1. \(\frac{\mathrm{g}}{4} \)
2. \(\frac{\mathrm{g}}{2} \)
3. \(\frac{3 \mathrm{~g}}{4} \)
4. g







