The electrostatic force between the metal plates of an isolated parallel plate capacitor \(C\) having a charge \(Q\) and area \(A\) is:

The diagrams below show regions of equipotentials.

A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:

A parallel-plate capacitor of area A, plate separation d, and capacitance C is filled with four dielectric materials having dielectric constants $k_1,k_2,k_3$ $$and $k_4$ as shown in the figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by

1. $\mathrm{k}={\mathrm{k}}_1+{\mathrm{k}}_2+{\mathrm{k}}_3+3{\mathrm{k}}_4$

2. $k=\frac{2}{3}\left(k_1+k_2+k_3\right)+2k_4$

3. $\frac{1}{k}=\frac{3}{2\left(k_1+k_2+k_3\right)}+\frac{1}{2k_4}$

4. $\frac{1}{\mathrm{k}}=\frac{1}{{\mathrm{k}}_1}+\frac{1}{{\mathrm{k}}_2}+\frac{1}{{\mathrm{k}}_3}+\frac{3}{2{\mathrm{k}}_4}$

A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \({S}\) is turned to position \(2,\) the percentage of its stored energy dissipated is:

       

1. \(20\%\)
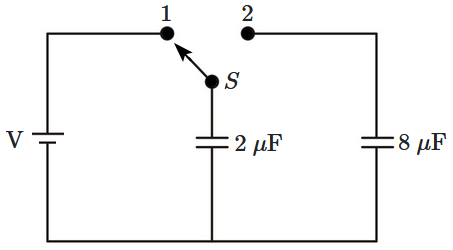
2. \(75\%\)
3. \(80\%\)
4. \(0\%\)