| 1. | connecting all of them in a series |
| 2. | connecting all of them in parallel |
| 3. | connecting two in series and one in parallel |
| 4. | connecting two in parallel and one in series |
An electrical circuit requires a capacitance of \(2~\mu\text{F}\) across a potential difference of \(1.0~\text{kV}.\) A large number of \(1~\mu\text{F}\) capacitors are available, each of which can withstand a maximum voltage of \(300~\text{V}.\) What is the minimum number of these capacitors needed to achieve the required capacitance and voltage rating?
1. \(2\)
2. \(16\)
3. \(24\)
4. \(32\)
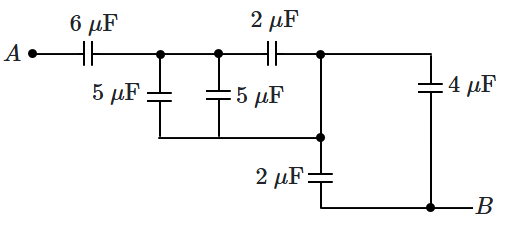
1. \(3.6~\mu \text F\)
2. \(2.4~\mu \text F\)
3. \(4.9~\mu \text F\)
4. \(5.4~\mu \text F\)
The figure shows the charge \((q)\) versus voltage \((V)\) graphs corresponding to two different combinations of the same pair of capacitors:
1. In parallel: \(A\)
2. In series: \(B\)
Based on the graphs (for \(A\) & \(B\)), what are the capacitances of the two capacitors?
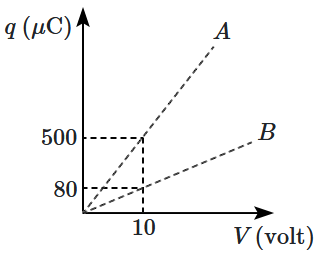
| 1. | \(50~ \mu \text{F} \text { and } 30 ~\mu \text{F}\) | 2. | \(40~ \mu \text{F} \text { and } 10 ~\mu \text{F}\) |
| 3. | \(20~ \mu \text{F} \text { and } 30 ~\mu \text{F}\) | 4. | \(60~ \mu \text{F} \text { and } 40 ~\mu \text{F}\) |
Two equal capacitors are first connected in series and then in parallel. The ratio of the equivalent capacitances, \(\left ( \dfrac{C_{Series}}{C_{Parallel}} \right )\) in these two cases will be:
1. \(4:1\)
2. \(2:1\)
3. \(1:4\)
4. \(1:2\)
Consider the combination of 2 capacitors \(\mathrm{C}_1\) and \(\mathrm{C}_2\), with \(\mathrm{C}_2>\mathrm{C}_1 \), when connected in parallel, the equivalent capacitance is \(\frac{15}{4}\)times the equivalent capacitance of the same connected in series. Calculate the ratio of capacitors,\(\frac{\mathrm{C}_2}{\mathrm{C}_1}\).
1. \(\frac{15}{11}\)
2. \(\frac{111}{80}\)
3. \(\frac{29}{15}\)
4. None of the above

1. \(2~\mu \text F\)
2. \(4~\mu \text F\)
3. \(6~\mu \text F\)
4. \(8~\mu \text F\)
1. \(2:1\)
2. \(1:2\)
3. \(1:4\)
4. \(4:1\)

1. \(\dfrac{C_1 C_2}{\left(C_1+C_2\right)} V \)
2. \(\dfrac{\left(C_1+C_2\right)}{C_1 C_2} V \)
3. \(\left({C}_1+{C}_2\right) {V} \)
4. \(\left({C}_1-{C}_2\right) {V}\)

| 1. | \(60~ \mu\text C\) | 2. | \(130 ~\mu\text C\) |
| 3. | \(260~ \mu \text C\) | 4. | \(585 ~\mu \text C\) |






