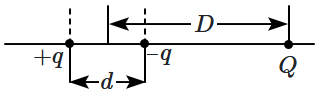
A system of three charges are placed as shown in the figure:
If \(D>>d\), the potential energy of the system is best given by:
1. \( \frac{1}{4 \pi \varepsilon_0}\left[+\frac{q^2}{d}+\frac{q Q d}{D^2}\right] \)
2. \( \frac{1}{4 \pi \varepsilon_0}\left[-\frac{q^2}{d}+\frac{q Q d}{D^2}\right] \)
3. \( \frac{1}{4 \pi \varepsilon_0}\left[-\frac{q^2}{d}+\frac{2 q Q d}{D^2}\right] \)
4. \( \frac{1}{4 \pi \varepsilon_0}\left[-\frac{q^2}{d}-\frac{q Q d}{D^2}\right] \)
A uniformly charged ring of radius \(3a\) and total charge \(q\) is placed in \(xy\)-plane centered at the origin. A point charge \(q\) is moving towards the ring along the \(z\)-axis and has speed \(v\) at \(z=4a\). The minimum value of \(v\) such that it crosses the origin is:
1. \( \sqrt{\frac{2}{m}}\left(\frac{1}{5} \frac{q^2}{4 \pi \varepsilon_0 {a}}\right)^{1 / 2} \)
2. \( \sqrt{\frac{2}{m}}\left(\frac{1}{15} \frac{q^2}{4 \pi \varepsilon_0 {a}}\right)^{1 / 2} \)
3. \( \sqrt{\frac{1}{m}}\left(\frac{1}{15} \frac{q^2}{4 \pi \varepsilon_0 {a}}\right)^{1 / 2} \)
4. \( \sqrt{\frac{2}{m}}\left(\frac{4}{5} \frac{q^2}{4 \pi \varepsilon_0 {a}}\right)^{1 / 2}\)
In free space, a particle \(A\) of charge \(1~\mu \text{C}\) is held fixed at a point \(P\). Another particle \(B\) of the same charge and mass \(4~\mu \text{g}\) is kept at a distance of \(1~\text{mm}\) from \(P\). If \(B\) is released, then its velocity at a distance of \(9~\text{mm}\) from \(P\) is:
\(\left[\text {Take} \frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 ~\text{Nm}^2 \text{C}^{-2}\right] \)
1. \(1.0 ~\text{m/s}\)
2. \(3.0 \times 10^4 ~\text{m/s}\)
3. \( 2.0 \times 10^3 ~\text{m/s} \)
4. \(6.2 \times 10^4 ~\text{m/s}\)
A two-point charges \(4q\) and \(-q\) are fixed on the x-axis at \(x=-\frac{d}{2}\) and \(x=\frac{d}{2}\), respectively. If a third point charge '\(q\)' is taken from the origin to \(x=d\) along the semicircle as shown in the figure, the energy of the charge will:
| 1. | increased by \(\frac{3 q^2}{4 \pi \varepsilon_0 \mathrm{~d}}\) |
| 2. | increase by \(\frac{2 q^2}{3 \pi \varepsilon_0 d}\) |
| 3. | decrease by \(\frac{4 q^2}{3 \pi \varepsilon_0 d}\) |
| 4. | decrease by \(\frac{q^2}{4 \pi \varepsilon_0 d}\) |
A solid sphere of radius \(R\) carries a charge (\(Q+q\)) distributed uniformly over its volume. A very small point like piece of it of mass \(m\) gets detached from the bottom of the sphere and falls down vertically under gravity. This piece carries charge \(q\). If it acquires a speed \(v\) when it has fallen through a vertical height \(y\) (see figure), then : (assume the remaining portion to be spherical).
1. \( v^2=2 y\left[\frac{q Q}{4 \pi \epsilon_0 \mathrm{R}(\mathrm{R}+\mathrm{y}) \mathrm{m}}+g\right] \)
2. \( v^2=y\left[\frac{q Q}{4 \pi \epsilon_0 \mathrm{R}^2 \mathrm{ym}}+g\right] \)
3. \( v^2=2 y\left[\frac{q Q R}{4 \pi \epsilon_0(\mathrm{R}+\mathrm{y})^3 \mathrm{~m}}+g\right] \)
4. \( v^2=y\left[\frac{q R}{4 \pi \epsilon_0 \mathrm{R}(\mathrm{R}+\mathrm{y}) \mathrm{m}}+g\right] \)
Two identical electric point dipoles have dipole moments \(\vec{P}_1=P\hat{i}\) and \(\vec{P}_2=-P\hat{i}\) and are held on the \(x\) axis at distance '\(a\)' from each other. When released, they move along the \(x\)-axis with the direction of their dipole moments remaining unchanged. If the mass of each dipole is '\(m\)', their speed when they are infinitely far apart is:
1. \( \frac{P}{a} \sqrt{\frac{1}{\pi \varepsilon_0 m a}} \)
2. \(\frac{P}{a} \sqrt{\frac{3}{2 \pi \varepsilon_0 \mathrm{ma}}} \)
3. \(\frac{P}{a} \sqrt{\frac{1}{2 \pi \varepsilon_0 m a}} \)
4. \(\frac{P}{a} \sqrt{\frac{2}{\pi \varepsilon_0 \mathrm{ma}}}\)
Twenty-seven identical spherical drops of mercury are each maintained at a potential of \(10~\text{V}.\) If all these drops coalesce to form a single large spherical drop, then the potential energy of this larger drop will be how many times that of one of the smaller drops?
| 1. | \(143\) | 2. | \(243\) |
| 3. | \(348\) | 4. | \(564\) |
1. \(\sqrt 2 : 1 \)
2. \(2\sqrt 2 : 1 \)
3. \(4\sqrt 2 : 1 \)
4. \(8:1\)

1. \(2\)
2. \(3\)
3. \(1\)
4. \(4\)