- 1(current)
Q. No.A thin convex lens made from crown glass \(\left(\mu=\frac{3}{2}\right) \) has focal length \(f\). When it is measured in two different liquids having refractive indices \(\frac{4}{3}\) and \(\frac{5}{3}\), it has the focal lengths \(f_1\) and \(f_2\) respectively. The correct relation between the focal lengths is:
| 1. | \(f_1>f\) and \(f_2\) becomes negative |
| 2. | \(f_2>f\) and \(f_1\) becomes negative |
| 3. | \(f_1\) and \(f_2\) becomes negative |
| 4. | \(f_1=f_2<f\) |
Subtopic: Lens Makers' Formula |
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A plano-convex lens and a plano-concave lens, which have the same radius of curvature \(R\) but are made of different materials, are placed side by side as shown in the figure. If the refractive index of the material of lens-\(1\) is \(\mu_1\) and that of lens-\(2\) is \(\mu_2,\) the focal length of the combined system is:
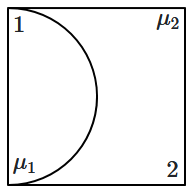
| 1. | \( \dfrac{R}{2-\left(\mu_1-\mu_2\right)} \) | 2. | \( \dfrac{R}{2\left(\mu_1-\mu_2\right)} \) |
| 3. | \( \dfrac{R}{\left(\mu_1-\mu_2\right)} \) | 4. | \( \dfrac{2 R}{\left(\mu_1-\mu_2\right)}\) |
Subtopic: Lens Makers' Formula |
55%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Two identical thin biconvex lenses of focal length 15 cm and refractive index 1.5 are in contact with each other. The space between the lenses is filled with a liquid of a refractive index 1.25. The focal length of the combination is:
1. 10 cm
2. 12 cm
3. 14 cm
4. 16 cm
1. 10 cm
2. 12 cm
3. 14 cm
4. 16 cm
Subtopic: Lens Makers' Formula |
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
The graph between \(\dfrac1u\) and \(\dfrac1v\) for a thin convex lens in order to determine its focal length is plotted as shown in the figure. The refractive index of the lens is \(1.5\) and both surfaces have the same radius of curvature \(R.\) The value of \(R\) will be: (where \(u\) = object distance, \(v\) = image distance)
1. \(10~\text{cm}\)
2. \(20~\text{cm}\)
3. \(30~\text{cm}\)
4. \(40~\text{cm}\)
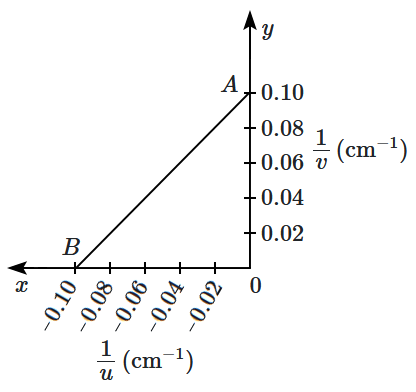
1. \(10~\text{cm}\)
2. \(20~\text{cm}\)
3. \(30~\text{cm}\)
4. \(40~\text{cm}\)
Subtopic: Lens Makers' Formula |
67%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A lens of refractive index \(1.5\) and focal length \(15\) cm in air is submerged in water. The focal length of the lens is: \(\left(\mu_w=\frac{4}{3}\right )\)
1. \(45\) cm
2. \(60\) cm
3. \(30\) cm
4. \(10\) cm
1. \(45\) cm
2. \(60\) cm
3. \(30\) cm
4. \(10\) cm
Subtopic: Lens Makers' Formula |
76%
JEE
Please attempt this question first.
Hints
Please attempt this question first.
If a biconvex lens of material of refractive index \(1.5\) has a focal length \(20~\text{cm}\) in air, then its focal length when it is submerged in a medium of refractive index \(1.6\) is:
1. \(-160~\text{cm}\)
2. \(160~\text{cm}\)
3. \(-1.6~\text{cm}\)
4. \(-16~\text{cm}\)
1. \(-160~\text{cm}\)
2. \(160~\text{cm}\)
3. \(-1.6~\text{cm}\)
4. \(-16~\text{cm}\)
Subtopic: Lens Makers' Formula |
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.