Consider a tightly wound \(100\) turn coil of radius \(10\) cm, carrying a current of \(1\) A. What is the magnitude of the magnetic field at the centre of the coil?

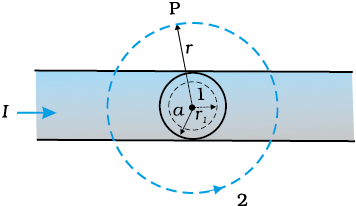
The figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. If the magnetic field in the region (r < a) is $B_1$ and for (r > a) is $B_2$, then $\frac{B_1}{B_2}$ is:

$1.<mspace\; width="1em"></mspace>\frac{a}{r}$
$2.<mspace\; width="1em"></mspace>\frac{a^2}{r^2}$
$3.<mspace\; width="1em"></mspace>\frac{r^2}{a^2}$
$4.<mspace\; width="1em"></mspace>\frac{r}{a}$

A solenoid of length \(0.5~\text m\) has a radius of \(1~\text{cm}\) and is made up of \(500\) turns. It carries a current of \(5~\text A.\) What is the magnitude of the magnetic field inside the solenoid?
1. \(6.28\times 10^{-3}~\text T\)
2. \(3.14\times 10^{-3}~\text T\)
3. \(2.72\times 10^{-3}~\text T\)
4. \(5.17\times 10^{-3}~\text T\)

A \(100\) turn closely wound circular coil of radius \(10~\text{cm}\) carries a current of \(3.2~\text{A}\). The magnetic field at the centre of the coil is:
1. \(4\times10^{-3}~\text{T}\)
2. \(6\times10^{-3}~\text{T}\)
3. \(2\times10^{-3}~\text{T}\)
4. \(5\times10^{-3}~\text{T}\)$\mathrm{}$

A solenoid has a core of material with relative permeability \(400.\) The windings of the solenoid are insulated from the core and carry a current of \(2~\text{A}.\) If the number of turns is \(1000\) per metre, the magnetizing current \(I_m\) is:
1. \(746~\text{A}\)
2. \(700~\text{A}\)
3. \(729~\text{A}\)
4. \(794~\text{A}\)