Q. No.Assume that an electric field \(\vec{E}=30x^2\hat{i}\) exists in space. Then the potential difference \(V_A-V_O\), where \(V_O\) is the potential at the original and \(V_A\) the potential at \(x=2~\text{m}\) is:
1. \(-120~\text{V}\)
2. \(-80~\text{V}\)
3. \(80~\text{V}\)
4. \(120~\text{V}\)
A parallel plate capacitor is made of two circular plates separated by a distance of \(5~\text{mm}\) and with a dielectric of dielectric constant \(2.2\) between them. When the electric field in the dielectric is \(3\times 10^4~\text{V/m}\), the charge density of the positive plate will be close to:
1. \( 3 \times 10^{-7} ~\text{C} / \text{m}^2 \)
2. \( 3 \times 10^4~\text{C} / \text{m}^2 \)
3. \( 6 \times 10^4 ~\text{C} / \text{m}^2 \)
4. \( 6 \times 10^{-7}~\text{C} / \text{m}^2 \)
A uniformly charged solid sphere of radius \(R\) has potential \(V_0\)
| 1. | \({R}_1=0 \text { and } {R}_2>\left({R}_4-{R}_3\right) \) |
| 2. | \({R}_1 \neq 0 \text { and }\left({R}_2-{R}_1\right)>\left({R}_4-{R}_3\right) \) |
| 3. | \({R}_1=0 \text { and } {R}_2<\left({R}_4-{R}_3\right) \) |
| 4. | \(2 {R}<{R}_4\) |
In the given circuit, charge \(Q_2\)
| 1. |  |
2. |  |
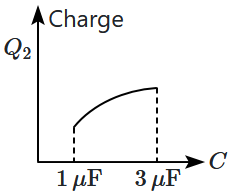| 3. |  |
4. |  |
| 1. | \(\begin{aligned} & \sigma_1 \neq 0, Q_1=0, ~~\text{and}~~\sigma_2 \neq 0, Q_2=0 \end{aligned}\) |
| 2. | \(\begin{aligned} & \sigma_1=0, Q_1=0,~~\text{and}~~ \sigma_2=0, Q_2=0 \end{aligned}\) |
| 3. | \(\begin{aligned} \sigma_1 & \neq 0, Q_1 \neq 0,~~\text{and}~~ \sigma_2 \neq 0, Q_2 \neq 0 \end{aligned}\) |
| 4. | \(\begin{aligned} & \sigma_1 \neq 0, Q_1=0, ~~\text{and}~~\sigma_2=0, Q_2=0 \end{aligned}\) |
1. \(5~\mu\text{C}\) from \({b}\) to \({a}\)
2. \({20}~\mu\text{C}\) from \({a}\) to \({b}\)
3. zero
4. \(5~\mu\text{C}\) from \({a}\) to \({b}\)
1. \({-110}~\text{J}\)
2. \({-140}~\text{J}\)
3. \({-120}~\text{J}\)
4. \({-130}~\text{J}\)
A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge \(Q\) (having a charge equal to the sum of the charges on the \(4~\mu \text{F}\) and \(9~\mu\text{F}\) capacitors), at a point distant \(30~\text{m}\) from it, would equal:
1. \(240~\text{N/C}\)
2. \(360~\text{N/C}\)
3. \(420~\text{N/C}\)
4. \(480~\text{N/C}\)
| 1. | connecting all of them in a series |
| 2. | connecting all of them in parallel |
| 3. | connecting two in series and one in parallel |
| 4. | connecting two in parallel and one in series |
A capacitance of \(2~\mu\text{F}\) is required in an electrical circuit across a potential difference of \(1.0~\text{kV}\). A large number of \(1~\mu\text{F}\) capacitors are available which can withstand a potential difference of not more than \(300~\text{V}\). The minimum number of capacitors required to achieve this is:
1. \(2\)
2. \(16\)
3. \(24\)
4. \(32\)
© 2025 GoodEd Technologies Pvt. Ltd.