Q. No.1. \(\frac{1}{4}~\text{Hz}\)
2. \(\dfrac{1}{2\sqrt2}~\text{Hz}\)
3. \(2~\text{Hz}\)
4. \(\dfrac{1}{2}~\text{Hz}\)
A block of mass \(m\) attched to a massless spring is performing oscillatory motion of amplitude '\(A\)' on a frictionless horizontal plane. If half of the mass of the block breaks off when it is passing through its equilibrium point, the amplitude of oscillation for the remaining system become \(fA\). The value of \(f\) is :
1. \( \sqrt{2} \)
2. \(1 \)
3. \(\frac{1}{2} \)
4. \(\frac{1}{\sqrt{2}}\)
An object of mass \(m\) is suspended at the end of a massless wire of length \(L\) and area of cross-section \(A.\) Young modulus of the material of the wire is \(Y.\) If the mass is pulled down slightly, its frequency of oscillation along the vertical direction is:
1.
2.
3.
4.
When a particle of mass \(m\) is attached to a vertical spring of spring constant \(k\) and released, its motion is described by \(y(t)=y_0 \sin ^2 \omega t\), where '\(y\)' is measured from the lower end of the unstretched spring. Then \(\omega\) is:
1. \( \sqrt{\frac{g}{y_0}} \)
2. \( \sqrt{\frac{g}{2 y_0}} \)
3. \( \frac{1}{2} \sqrt{\frac{g}{y_0}} \)
4. \( \sqrt{\frac{2 g}{y_0}} \)
In the given figure, mass \(M\) is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is \(k\). The mass oscillates on a frictionless surface with time period \(T\) and amplitude \(A\). When the mass is in an equilibrium position, as shown in the figure, another mass \(m\) is gently fixed upon it. The new amplitude of oscillation will be:
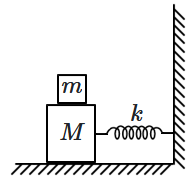
1. \( A \sqrt{\frac{M-m}{M}} \)
2. \(A \sqrt{\frac{M}{M+m}} \)
3. \(A \sqrt{\frac{M+m}{M}} \)
4. \( A \sqrt{\frac{M}{M-m}} \)
In the given figure, a body of mass \(M\) is held between two massless springs, on a smooth inclined plane. The free ends of the springs are attached to firm supports. If each spring has spring constant \(k,\) the frequency of oscillation of given body is :
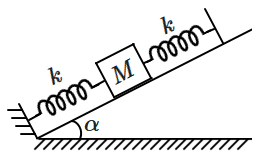
| 1. | \(\dfrac{1}{2 \pi} \sqrt{\dfrac{k}{2 M}}\) | 2. | \(\dfrac{1}{2 \pi} \sqrt{\dfrac{2 {k}}{{Mg\sin} \alpha}}\) |
| 3. | \(\dfrac{1}{2 \pi} \sqrt{\dfrac{2 k}{M}}\) | 4. | \(\dfrac{1}{2 \pi} \sqrt{\dfrac{ {k}}{{Mg\sin} \alpha}}\) |
Two identical springs of spring constant '\(2k\)' are attached to a block of mass \(m\) and to fixed support (see figure). When the mass is displaced from the equilibrium position on either side, it executes simple harmonic motion. The time period of oscillation of this system is:
1. \(2\pi \sqrt{\frac{m}{k}}\)
2. \(\pi \sqrt{\frac{m}{2k}}\)
3. \(2\pi \sqrt{\frac{m}{2k}}\)
4. \(\pi \sqrt{\frac{m}{k}}\)
1. \(1:2\)
2. \(3:2\)
3. \(3:1\)
4. \(2:3\)
1. \(\frac{T_{1}}{T_{2}}=\frac{3}{\sqrt{2}}\)
2. \(\frac{T_{1}}{T_{2}}=\sqrt{\frac{3}{2}} \)
3. \(\frac{T_{1}}{T_{2}}=\sqrt{\frac{2}{3}} \)
4. \(\frac{T_{1}}{T_{2}}=\frac{\sqrt{2}}{3}\)
| 1. | \(2\pi \sqrt{\dfrac{1}{20}}\) s | 2. | \(\pi \sqrt{\dfrac{1}{20}}\) s |
| 3. | \(2\pi \sqrt{\dfrac{1}{10}}\) s | 4. | \(\pi \sqrt{\dfrac{1}{10}}\) s |
© 2025 GoodEd Technologies Pvt. Ltd.