Q. No.Two coaxial solenoids of different radii carry current \(I\) in the same direction. Let \(\vec{F}_1\) be the magnetic force on the inner solenoid due to the outer one and \(\vec{F}_2\) be the magnetic force on the outer solenoid due to the inner one. Then:
| 1. | \(\overrightarrow{{F}_1}=\overrightarrow{F_2}=0\) |
| 2. | \(\vec{F}_1\) is radially inwards and \(\vec{F}_2\) is radially outwards |
| 3. | \(\vec{F}_1\) is radially inwards and \(\vec{F}_2=0\) |
| 4. | \(\vec{F}_1\) is radially outwards and \(\vec{F}_2=0\) |
Two long current carrying thin wires, both with current \(I\), are held by insulating threads of length \(L\) and are in equilibrium as shown in the figure, with threads making an angle '\(\theta\)' with the vertical. The mass per unit length of wires is \(\lambda\), then the value of \(I\) is:
(\(g=\) gravitational acceleration)
1. \( \sin \theta \sqrt{\frac{\pi \lambda g L}{\mu_0 \cos \theta}} \)
2. \( 2 \sin \theta \sqrt{\frac{\pi \lambda g L}{\mu_0 \cos \theta}} \)
3. \( 2 \sqrt{\frac{\pi g L}{\mu_0} \tan \theta} \)
4. \( 2 \sqrt{\frac{\pi \lambda g L}{\mu_0} \tan \theta}\)
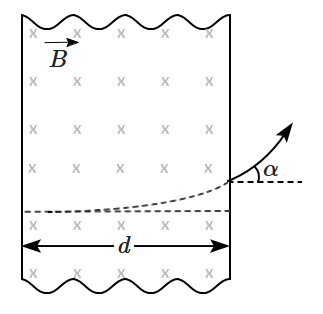
1. \(\frac{B}{d} \sqrt{\frac{q}{2 m V}}\)
2. \(B d \sqrt{\frac{q}{2 m V}}\)
3. \(\frac{B}{2} \sqrt{\frac{q d}{m V}}\)
4. \(q V \sqrt{\frac{B d}{2 m}}\)
1. \({IBR\over 2\sin\theta_0}\)
2. \({IBR\theta_0\over \sin\theta_0}\)
3. \({IBR}\)
4. \({IBR\over \sin\theta_0}\)
| 1. |  |
3. |  |
| 2. |  |
4. |  |
(Given \({\mu_0\over 4\pi}=10^{-7}\) in \(\text{S.I.}\) units and \({B_H}=\) Horizontal component of earth's magnetic field \(=3.6\times10^{-5}\) Tesla)
1. \(14.6\)
2. \(19.4\)
3. \(9.7\)
4. \(4.9\)
| 1. | hot wire voltmeter |
| 2. | moving coil galvanometer |
| 3. | potential coil galvanometer |
| 4. | moving magnet galvanometer |
Two identical wires \(\mathrm{A}\) and \(\mathrm{B}\), each of length '\(l\)', carry the same current \(I\). Wire \(\mathrm{A}\) is bent into a circle of radius \(R\) and wire \(\mathrm{B}\) is bent to form a square of side '\(a\)'. If \(B_A\) and \(B_B\) are the values of the magnetic field at the centres of the circle and square respectively, then the ratio \(\frac{B_A}{B_B}\) is?
1. \( \frac{\pi^2}{8} \)
2. \( \frac{\pi^2}{16 \sqrt{2}} \)
3. \( \frac{\pi^2}{16} \)
4. \( \frac{\pi^2}{8 \sqrt{2}} \)
A galvanometer having a coil resistance of \(100~\Omega\) gives a full-scale deflection when a current of \(1~\text{mA}\) is passed through it. The value of the resistance which can convert this galvanometer into an ammeter giving a full-scale deflection for a current of \(10~\text{A}\), is:
1. \(0.01~\Omega\)
2. \(2~\Omega\)
3. \(0.1~\Omega\)
4. \(3~\Omega\)
When a current of \(5~\text{mA}\) is passed through a galvanometer having a coil of resistance \(15~\Omega\), it shows full scale deflection. The value of the resistance to be put in series with the galvanometer to convert it into a voltmeter of range \(0\text{-}10~\text{V}\) is:
1. \( 1.985 \times 10^3 ~\Omega \)
2. \( 2.045 \times 10^3 ~\Omega \)
3. \( 2.535 \times 10^3 ~\Omega \)
4. \( 4.005 \times 10^3 ~\Omega\)
© 2025 GoodEd Technologies Pvt. Ltd.