Q. No.| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | speed which is \(\frac{3}{4}\text{th}\) of that of the roller when the weight is \(0.4~\text{m}\) above the ground |
| 2. | constant speed |
| 3. | decreasing speed |
| 4. | increasing speed |
Ship \(A\) is sailing towards north-east with velocity \(\vec{v}=30 \hat{i}+50 \hat{j}+50 \hat{i}~ \text{km/hr}\) where \(\hat{i}\) and \(\hat{j}\) north. Ship \(B\) is at a distance of \(80~\text{km}\) east and \(150~\text{km}\) north of Ship \(A\) and is sailing towards west at \(10~\text{km/hr}\). \(A\) will be at minimum distance from \(B\) in:
1. \(4.2~\text{hrs}\)
2. \(2.2~\text{hrs}\)
3. \(2.6~\text{hrs}\)
4. \(3.2~\text{hrs}\)
The stream of a river is flowing with a speed of \(2~\text{km/h}\). A swimmer can swim at a speed of \(4~\text{km/h}\). What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
1. \( 60^{\circ} \)
2. \( 90^{\circ} \)
3. \( 150^{\circ} \)
4. \( 120^{\circ}\)
\(\vec{r}(t)=(15 t^2) \hat{i}+\left(4-20 t^2\right) \hat{j},\) where \(\vec{r}(t)\) is in metres and \(t\) is in seconds.
What is the magnitude of the acceleration at \(t=1\) second?
| 1. | \(100\) m/s2 | 2. | \(40\) m/s2 |
| 3. | \(50\) m/s2 | 4. | \(25\) m/s2 |
A plane is inclined at an angle \(\alpha =30^\circ\) with respect to the horizontal. A particle is projected with a speed \(u=2~\text{ms}^{-1}\), from the base of the plane, making an angle \(\theta=15^\circ\) with respect to the plane as shown in the figure. the distance from the base, at which the particle hits the plane is close to: (Take \(g= 10\) ms–2)
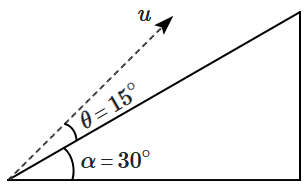
1. \(14~\text{cm}\)
2. \(18~\text{cm}\)
3. \(20~\text{cm}\)
4. \(26~\text{cm}\)
A shell is fired from a fixed artillery gun with an initial speed \(u\) such that it hits the target on the ground at a distance \(R\) from it. If \(t_1\) and \(t_2\) are the values of the time taken by it to hit the target in two possible ways, the product \(t_1t_2\) is:
1. \(\frac{2R}{g}\)
2. \(\frac{R}{2g}\)
3. \(\frac{R}{g}\)
4. \(\frac{R}{4g}\)
The trajectory of a projectile near the surface of the earth is given as \(y=2x-9x^2\). If it were launched at an angle \(\theta_0\) with speed \(v_0\) then:\(\left(g= 10~\text{ms}^{-2}\right)\)
| 1. | \(\theta_0=\cos^{-1}\left(\frac{1}{\sqrt{5}}\right) \text{ and }v_0=\frac{5}{3}~\text{ms}^{-1}\) |
| 2. | \(\theta_0=\cos^{-1}\left(\frac{2}{\sqrt{5}}\right) \text{ and }v_0=\frac{3}{5}~\text{ms}^{-1}\) |
| 3. | \(\theta_0=\sin^{-1}\left(\frac{2}{\sqrt{5}}\right) \text{ and }v_0=\frac{3}{5}~\text{ms}^{-1}\) |
| 4. | \(\theta_0=\sin^{-1}\left(\frac{1}{\sqrt{5}}\right) \text{ and }v_0=\frac{5}{3}~\text{ms}^{-1}\) |
Two particles are projected from the same point with the same speed \(u,\) but at different angles. They both cover the same horizontal range \(R,\) but reach different maximum heights, \(h_1\) and \(h_2.\) Which of the following relations is correct?
1. \(R^2=h_1h_2\)
2. \(R^2=16h_1h_2\)
3. \(R^2=4h_1h_2\)
4. \(R^2=2h_1h_2\)
1. \(y=x^2+\text{constant}\)
2. \(y^2=x+\text{constant}\)
3. \(y^2=x^2+\text{constant}\)
4. \(xy=\text{constant}\)
© 2025 GoodEd Technologies Pvt. Ltd.