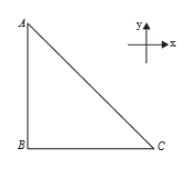
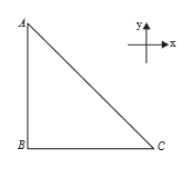
A current-carrying closed Loop in the form of a right isosceles triangle ABC is placed in xy plane in a uniform magnetic field acting along the y-axis as shown in the figure. If the magnetic force on the arm AC is $\overrightarrow{F}$, then force on the arm BC and AB are respectively

1. zero, zero 
2. \(-\vec {F}\) and zero 
3. \(\vec {F}\) and \(-\vec {F}\)
4. \(\vec {F}\) and zero

समकोण समद्विबाहु त्रिभुज ABC के रूप में एक धारावाही बंद लूप को Y-अक्ष के अनुदिश आरोपित एकसमान चुंबकीय क्षेत्र में  XY -तल में चित्र में दर्शाए गए अनुसार स्थित है। यदि भुजा AC पर चुंबकीय बल $\overrightarrow{F}$ है, तब भुजा BC और AB पर आरोपित बल क्रमशः है -

1.  शून्य, शून्य
2. \(-\vec {F}\) और शून्य
3. \(\vec {F}\) और \(-\vec {F}\)
4. \(\vec {F}\) और शून्य

When a proton is released from rest in a room, it starts with an initial acceleration ${\mathrm{a}}_0$ towards the east. When it is projected towards the north with a speed ${\mathrm{v}}_0$, it moves with initial acceleration $3{\mathrm{a}}_0$ towards east. The electric and magnetic fields in the room are-
1. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \text {west, }\frac{\mathrm{Ma}_0}{\mathrm{ev}_0} \mathrm{up} \)
2. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \text { west,} \frac{2 \mathrm{Ma}_0}{\mathrm{ev}_0} \text {down} \)
3. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \text {east, } \frac{2 \mathrm{Ma}_0}{\mathrm{ev}_0} \text { down} \)
4. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \text { east, }\frac{2 \mathrm{Ma}_0}{\mathrm{ev}_0} \text {up}\)

जब एक प्रोटॉन को कमरे में विरामावस्था से मुक्त किया जाता है, तब यह पूर्व की ओर  प्रारंभिक त्वरण ${\mathrm{a}}_0$ से गति करता है। जब इसे ${\mathrm{v}}_0$ वेग से उत्तर की ओर प्रक्षेपित किया जाता है, तब यह $3{\mathrm{a}}_0$ प्रारंभिक त्वरण से पूर्व की ओर गति करता है। कमरे में विद्युत और चुंबकीय क्षेत्र क्रमश: हैं -
1. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \) पश्चिम , \(\frac{\mathrm{Ma}_0}{\mathrm{ev}_0}\)ऊपर
2. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \)पश्चिम , \(\frac {2Ma_0}{ev_0}\)नीचे
3. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \)पूर्व, \(\frac {2Ma_0}{ev_0}\)नीचे
4. \(\frac{\mathrm{Ma}_0}{\mathrm{e}} \) पूर्व, \(\frac {2Ma_0}{ev_0}\)ऊपर

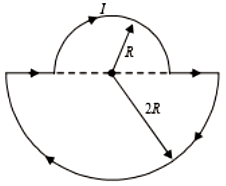
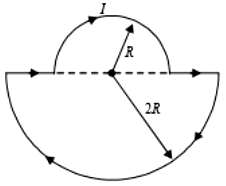
The magnetic dipole moment of the given loop is 

                 
1. \(\frac{5}{2} \pi \text R^2 \text I \)
2. \(3 \pi \text R^2 \text I \)
3. \(\frac{3}{2} \pi \text R^2 \text I \)
4. \(5 \pi \text R^2 \text I\)

दिए गये लूप का चुंबकीय द्विध्रुव आघूर्ण है:

 1. \(\frac{5}{2} \pi \text R^2 \text I \)
2. \(3 \pi \text R^2 \text I \)
3. \(\frac{3}{2} \pi \text R^2 \text I \)
4. \(5 \pi \text R^2 \text I\)

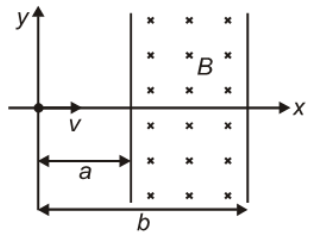
The figure shows a particle of charge q and mass m moving with velocity v along the x-axis enters a region of the uniform magnetic field. The minimum value of v so that the charge q is deflected by an angle $30°$ is

                                       
1. \(\frac{2 \mathrm{qBb}-\mathrm{a}}{\mathrm{m}} \)
2. \(\frac{\mathrm{qBb}+\mathrm{a}}{2 \mathrm{~m}} \)
3. \(\frac{\mathrm{qBb}-\mathrm{a}}{\mathrm{m}} \)
4. \(\frac{\mathrm{qBb}}{2 \mathrm{~m}}\)

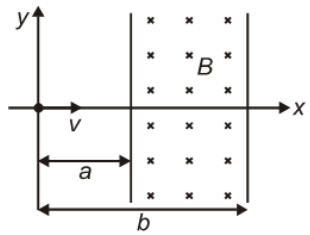
चित्र एक समान चुंबकीय क्षेत्र में x-अक्ष के अनुदिश v वेग से प्रवेश करने वाले  q आवेश और m द्रव्यमान के एक कण को दर्शाता है। वेग v का न्यूनतम मान जिससे कण, $30°$ के कोण से विक्षेपित होता है।  

 1. \(\frac{2 \mathrm{qBb}-\mathrm{a}}{\mathrm{m}} \)
2. \(\frac{\mathrm{qBb}+\mathrm{a}}{2 \mathrm{~m}} \)
3. \(\frac{\mathrm{qBb}-\mathrm{a}}{\mathrm{m}} \)
4. \(\frac{\mathrm{qBb}}{2 \mathrm{~m}}\)

An infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of i ampere and the radius of the circular loop is r meter. Then the magnetic induction at its centre will be 

1. $\frac{{\mu }_0}{4\mathrm{\pi }}\frac{2i}{r}(\mathrm{\pi }+1)$
2. $\frac{{\mu }_0}{4\mathrm{\pi }}\frac{2i}{r}(\mathrm{\pi }-1)$
3. Zero
4. Infinite

एक अनंत लंबाई के सीधे चालक तार को चित्र में दिखाई गई आकृति के अनुसार मोड़ा गया है। इसमें i ऐम्पियर की धारा प्रवाहित होती है और वृत्ताकार लूप की त्रिज्या r मीटर है। तब इसके केंद्र पर चुंबकीय क्षेत्र होगा-

1. $\frac{{\mu }_0}{4\mathrm{\pi }}\frac{2i}{r}(\mathrm{\pi }+1)$
2. $\frac{{\mu }_0}{4\mathrm{\pi }}\frac{2i}{r}(\mathrm{\pi }-1)$
3. शून्य
4. अनंत

In the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be $\left(\theta =\frac{\pi }{n}\right)$

1. $\frac{{\mu }_{o}i}{2\mathrm{\pi a}}\tan \frac{\mathrm{\pi }}{n}$   

2. $\frac{{\mu }_{0}ni}{2\mathrm{\pi a}}\tan \frac{\mathrm{\pi }}{n}$

3.$\frac{2}{\mathrm{\pi }}\frac{ni}{a}{\mu }_0\tan \frac{\mathrm{\pi }}{n}$ 

4. $\frac{ni}{2a}{\mu }_0\tan \frac{\mathrm{\pi }}{n}$

निम्नलिखित आकृति में एक तार a त्रिज्या वाले वृत्त से घिरे एक n भुजा के एक नियमित बहुभुज के रूप में मुड़ा हुआ है। केंद्र पर कुल चुंबकीय क्षेत्र होगा: $\left(\theta =\frac{\pi }{n}\right)$

1. $\frac{{\mu }_{o}i}{2\mathrm{\pi a}}\tan \frac{\mathrm{\pi }}{n}$

2. $\frac{{\mu }_{0}ni}{2\mathrm{\pi a}}\tan \frac{\mathrm{\pi }}{n}$

3.$\frac{2}{\mathrm{\pi }}\frac{ni}{a}{\mu }_0\tan \frac{\mathrm{\pi }}{n}$ 

4. $\frac{ni}{2a}{\mu }_0\tan \frac{\mathrm{\pi }}{n}$

A part of a long wire carrying a current i is bent into a circle of radius r as shown in the figure. The net magnetic field at the centre O of the circular loop is

1. $\frac{{\mu }_{0}i}{4r}$

2. $\frac{{\mu }_{0}i}{2\mathrm{\pi r}}\left(\mathrm{\pi }+1\right)$

3. $\frac{{\mu }_{0}i}{2r}$ 

4. $\frac{{\mu }_{0}i}{2\mathrm{\pi r}}\left(\mathrm{\pi }-1\right)$

धारा i वाले लंबे तार का एक भाग त्रिज्या r के एक वृत्त के रूप में मुड़ा हुआ है जैसा कि चित्र में दिखाया गया है। वृत्ताकार लूप के केंद्र O पर कुल चुंबकीय क्षेत्र है: 

1. $\frac{{\mu }_{0}i}{4r}$ 
       
2. $\frac{{\mu }_{0}i}{2\mathrm{\pi r}}\left(\mathrm{\pi }+1\right)$

3. $\frac{{\mu }_{0}i}{2r}$         

4. $\frac{{\mu }_{0}i}{2\mathrm{\pi r}}\left(\mathrm{\pi }-1\right)$

A and B are two concentric circular conductors of centre O and carrying currents ${\mathrm{i}}_{1<mspace\; width="1em"></mspace>}<mspace\; width="1em"></mspace>$and ${\mathrm{i}}_2$ as shown in the adjacent figure. If ratio of their radii is 1 : 2 and ratio of the flux densities at O due to A and B is 1 : 3, then the value of ${\mathrm{i}}_1/{\mathrm{i}}_2$ is

1.  $\frac{1}{6}$     
                 
2.  $\frac{1}{4}$                                

3.  $\frac{1}{3}$         
             
4.  $\frac{1}{2}$                                                                                                          

A और B समान केंद्र O वाले दो संकेंद्रित वृत्ताकार चालक हैं और जिनमें धाराएँ ${\mathrm{i}}_{1<mspace\; width="1em"></mspace>}<mspace\; width="1em"></mspace>$और ${\mathrm{i}}_2$ प्रवाहित हो रही हैं जैसा कि आसन्न आकृति में दिखाया गया है। यदि उनकी त्रिज्या का अनुपात 1: 2 है और A और B के कारण O पर फ्लक्स घनत्व का अनुपात 1: 3 है, तब ${\mathrm{i}}_1/{\mathrm{i}}_2$ का मान है:

1.  $\frac{1}{6}$   

2. $\frac{1}{4}$

3. $\frac{1}{3}$                 
           
4. $\frac{1}{2}$          

PQRS is a square loop made of uniform conducting wire the current enters the loop at P and leaves at S. Then the magnetic field will be

PQRS एकसमान चालक तार से निर्मित एक वर्गाकार लूप है, धारा लूप में P से प्रवेश करती है और S से निकलती है। तब चुंबकीय क्षेत्र होगा:

A proton and an $\mathrm{\alpha }-$ particle enter a uniform magnetic field perpendicularly with the same speed. If proton takes 25 $\mathrm{\mu }$ sec to make 5 revolutions, then the periodic time for the $\mathrm{\alpha }-$particle would be :

1. 50 $\mathrm{\mu }$ sec               
2. 25 $\mathrm{\mu }$ sec 
3. 10 $\mathrm{\mu }$ sec                 
4. 5 $\mathrm{\mu }$ sec

एक प्रोटॉन और एक $\mathrm{\alpha }$$-$कण एक समान गति से एक समान चुंबकीय क्षेत्र में लंबवत् रूप से प्रवेश करते हैं। यदि प्रोटॉन 5 घूर्णन करने के लिए $25\mathrm{\mu <mspace\; width="1em"></mspace>}sec$लेता है, तब $\mathrm{\alpha }$$-$कण के लिए आवर्त काल कितना होगा:

1. 50 $\mathrm{\mu }$$sec$             
2. 25$\mathrm{\mu }$$sec$  
3. 10 $\mathrm{\mu }$$sec$             
4. 5$\mathrm{\mu }$$sec$