A projectile is fired at angle $\mathrm{\theta }$ with horizontal with initial speed u. If it breaks into two halves such that one half retraces its path, then the distance of hitting point of the other half from starting point is

1. $\frac{{\mathrm{u}}^2\sin 2\mathrm{\theta }}{\mathrm{g}}$

2. $\frac{2{\mathrm{u}}^2\sin 2\mathrm{\theta }}{\mathrm{g}}$

3. $\frac{{\mathrm{u}}^2\sin 2\mathrm{\theta }}{2\mathrm{g}}$

4. $\frac{{\mathrm{u}}^2\mathrm{sin\theta }}{2\mathrm{g}}$

एक प्रक्षेप्य को u प्रारम्भिक वेग से क्षैतिज के साथ $\theta$ कोण पर प्रक्षेपित किया जाता है। यदि यह दो भागों में इस प्रकार विभाजित होता है कि एक भाग अपने पथ को पुनः अनुरेखित करता है, प्रारम्भिक बिंदु से दूसरे भाग के संघट्ट बिंदु की दूरी ज्ञात कीजिए।

1. $\frac{u^2\sin <mspace\; width="1em"></mspace>2\theta }{g}$

2. $\frac{2u^2\sin 2\theta }{g}$

3. $\frac{u^2\sin 2\theta }{2g}$

4. $\frac{u^2\sin \theta }{2g}$

The moment of inertia of a cube of mass m and side a about one of its edges is equal to

1. $\frac{\mathrm{}}{}$\(\frac{2}{3}~ma^{2}\)              

2.  \(\frac{4}{3}~ ma^{2}\)$\frac{\mathrm{}}{}$

3. $\mathrm{}$\(3~ma^{2}\)                

4. \(\frac{8}{3}~ ma^{2}\)$\frac{\mathrm{}}{}$

द्रव्यमान m तथा भुजा a के घन का इसकी किसी एक भुजा के परितः जड़त्व आघूर्ण किसके बराबर है?
1. \(\frac{2}{3}~ma^{2}\) 
2. \(\frac{4}{3}~ ma^{2}\)
3. \(3~ma^{2}\) 
4. \(\frac{8}{3}~ ma^{2}\)

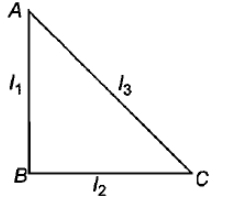
ABC is a right angled triangular plate of uniform thickness. The sides are such that AB > BC as shown in figure.
\(\mathrm{I}_{1},\mathrm{I}_{2}\) and \(\mathrm{I}_3\) are moments of inertia about AB, BC and AC respectively. Then, which of the following relation is correct?
 

1. \(\mathrm{I}_{1}=\mathrm{I}_{2}=\mathrm{I}_{3}\)
2. \(\mathrm{I}_2>\mathrm{I}_1>\mathrm{I}_3\)
3. \(1_{3}<1_{2}<1_{1}\)
4. \(I_{3}>I_{1}>I_{2}\)$\mathrm{}$






 

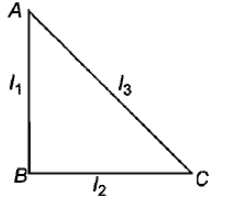
ABC एकसमान मोटाई की समकोण त्रिभुजाकार प्लेट है, जिसकी भुजाएँ इस प्रकार हैं कि AB > BC, जैसा कि आकृति में दर्शाया गया है। ${\mathrm{}}_{}$
\(\mathrm{I}_{1},\mathrm{I}_{2}\) और \(\mathrm{I}_3\)${\mathrm{}}_{}$ क्रमशः AB, BC और AC के परितः जड़त्व आघूर्ण हैं। तब, निम्नलिखित में से कौन-सा संबंध सत्य है?
 

 1. \(\mathrm{I}_{1}=\mathrm{I}_{2}=\mathrm{I}_{3}\)
2. \(\mathrm{I}_2>\mathrm{I}_1>\mathrm{I}_3\)
3. \(1_{3}<1_{2}<1_{1}\)
4. \(I_{3}>I_{1}>I_{2}\)

For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of gravity and perpendicular to the plane of the body?

1. A disc of radius a

2. a ring of radius a

3. a square lamina of side 2 a

4. four rods forming square of side 2 a.

कुल समान द्रव्यमान के लिए, गुरुत्व केंद्र से गुजरने वाली और पिंड के तल के लंबवत अक्ष के परितः निम्नलिखित में से किसका जड़त्व आघूर्ण सर्वाधिक होगा?

1. a त्रिज्या की चकती का  

2. a त्रिज्या के वलय का 

3. 2 a भुजा के वर्ग पटल का

4. 2 a भुजा के वर्ग का निर्माण कर रही चार छड़ों का

Two Circular discs A and B are of equal masses and thicknesses but made of metal with densities ${\mathrm{d}}_{\mathrm{A}}<mspace\; width="1em"></mspace>\mathrm{and}<mspace\; width="1em"></mspace>{\mathrm{d}}_{\mathrm{B}}$ (${\mathrm{d}}_{\mathrm{A}}<mspace\; width="1em"></mspace>><mspace\; width="1em"></mspace>{\mathrm{d}}_{\mathrm{B}}$). If their moments of inertia about an axis passing through their centers and perpendicular to circular faces be ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>\mathrm{and}<mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$, then

1.  ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>=<mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$

2.  ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>><mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$

3.  ${\mathrm{I}}_{\mathrm{A}}\hspace{0.17em}<\hspace{0.17em}{\mathrm{I}}_{\mathrm{B}}$

4.  ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>\ge <mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$

दो वृताकार डिस्कों A और B, समान द्रव्यमान और समान मोटाई की हैं, परन्तु ${\mathrm{d}}_{\mathrm{A}}<mspace\; width="1em"></mspace><mspace\; width="1em"></mspace>\text{और}<mspace\; width="1em"></mspace><mspace\; width="1em"></mspace>{\mathrm{d}}_{\mathrm{B}}$ (${\mathrm{d}}_{\mathrm{A}}<mspace\; width="1em"></mspace>><mspace\; width="1em"></mspace>{\mathrm{d}}_{\mathrm{B}}$) घनत्व की धातुओं से बनाई गई हैं। यदि इनके केंद्रों से होकर गुजरने वाली तथा इनके तल के लम्बवत अक्षों के परितः जड़त्व आघूर्ण ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace><mspace\; width="1em"></mspace>\text{और}<mspace\; width="1em"></mspace><mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$ हैं, तब:

1.  ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>=<mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$

2.  ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>><mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$

3.  ${\mathrm{I}}_{\mathrm{A}}\hspace{0.17em}<\hspace{0.17em}{\mathrm{I}}_{\mathrm{B}}$

4.  ${\mathrm{I}}_{\mathrm{A}}<mspace\; width="1em"></mspace>\ge <mspace\; width="1em"></mspace>{\mathrm{I}}_{\mathrm{B}}$

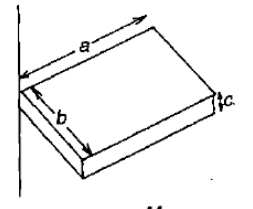
The figure shows a uniform solid block of mass M and edge lengths a, b and c. Its M.O.I. about an axis through one edge and perpendicular (as shown) to the large face of the block is 

1. $\frac{M}{3}\left(a^2+b^2\right)$

2. $\frac{M}{4}\left(a^2+b^2\right)$

3. $\frac{7M}{12}\left(a^2+b^2\right)$

4. $\frac{M}{12}\left(a^2+b^2\right)$

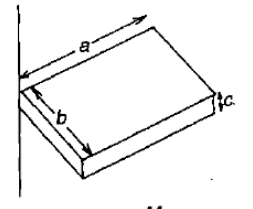
चित्र m द्रव्यमान और a, b व c लम्बाई की भुजाओं के एकसमान ठोस गुटके को दर्शाता है। भुजा c से गुजरने वाले और गुटके के बड़े फलक के लंबवत (जैसा कि दर्शाया गया है) अक्ष के परितः इसका जड़त्व आघूर्ण ज्ञात कीजिए।

1. $\frac{M}{3}\left(a^2+b^2\right)$

2. $\frac{M}{4}\left(a^2+b^2\right)$

3. $\frac{7M}{12}\left(a^2+b^2\right)$

4. $\frac{M}{12}\left(a^2+b^2\right)$

From a uniform square plate of side a and mass m, a square portion DEFG of side $\frac{\mathrm{a}}{2}$ is removed. Then, the moment of inertia of the remaining portion about the axis AB is

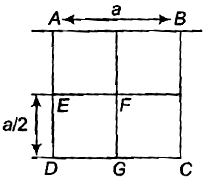
1. \(\dfrac{7ma^2}{16}\)
2. \(\dfrac{3ma^2}{16}\)
3. \(\dfrac{3ma^2}{4}\)
4. \(\dfrac{9ma^2}{16}\)

a भुजा और m द्रव्यमान की एकसमान वर्गाकार प्लेट से, $\frac{\mathrm{a}}{2}$ भुजा के एक वर्गाकार भाग DEFG को निकाला जाता है। तब, अक्ष AB के परितः शेष भाग का जड़त्व आघूर्ण ज्ञात कीजिए।

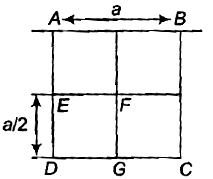
 1. \(\dfrac{7ma^2}{16}\)
2. \(\dfrac{3ma^2}{16}\)
3. \(\dfrac{3ma^2}{4}\)
4. \(\dfrac{9ma^2}{16}\)

A uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing thorugh A and Perpendicular to the plane of paper is

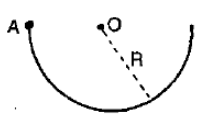
1. $\frac{2}{3}M{R}^2$

2. $M{R}^2$

3. 2$M{R}^2$

4. $\frac{3}{2}M{R}^2$

द्रव्यमान m की एकसमान छड़ को त्रिज्या R के अर्धवृत्त के रूप में मोड़ा जाता है। A से गुजरने वाली और कागज के तल के लंबवत अक्ष के परितः छड़ का जड़त्व आघूर्ण ज्ञात कीजिए।

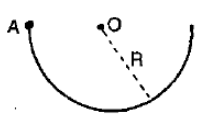
1. $\frac{2}{3}M{R}^2$

2. $M{R}^2$

3. 2$M{R}^2$

4. $\frac{3}{2}M{R}^2$

A force 2N is along line y = 3x + 4. The torque about the origin is:

1.  $\frac{5}{\sqrt{10}}\mathrm{Nm}$

2.  $\frac{7}{\sqrt{10}}\mathrm{Nm}$

3.  $\frac{6}{\sqrt{10}}\mathrm{Nm}$

4.  $\frac{8}{\sqrt{10}}\mathrm{Nm}$

एक बल 2N, रेखा y = 3x + 4 के अनुदिश है। मूल-बिंदु के परितः बल आघूर्ण है:

1.  $\frac{5}{\sqrt{10}}\mathrm{Nm}$

2.  $\frac{7}{\sqrt{10}}\mathrm{Nm}$

3.  $\frac{6}{\sqrt{10}}\mathrm{Nm}$

4.  $\frac{8}{\sqrt{10}}\mathrm{Nm}$

A bob of mass m attached to an inextensible string of length l is suspended from verticle support.  The bob rotates in a horizontal circle with an angular speed $\mathrm{\omega }<mspace\; width="1em"></mspace>\mathrm{rad}/\mathrm{s}$ about the vertical.  About the point of suspension.

l लंबाई की अवितान्य डोरी से जुड़े m द्रव्यमान के गोलक को ऊर्ध्वाधर आधार से निलंबित किया जाता है। गोलक $\mathrm{\omega }<mspace\; width="1em"></mspace>\mathrm{rad}/\mathrm{s}$ के कोणीय वेग के साथ ऊर्ध्वाधर अक्ष के परितः क्षैतिज वृत्त में घूर्णन करता है। निलंबन बिंदु के परितः