- 1(current)
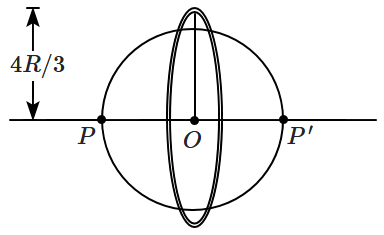
Q. No.A uniform solid sphere of mass \(M\) and radius \(R\) has a thin uniform ring of mass \(\dfrac{5M}{3}\) and radius \(\dfrac{4R}{3}\) around it. The two objects have a common centre \(O,\) and the axis of the ring \((PP')\) lies along a diameter of the sphere. Physical quantities associated with this system are mentioned in Column-I and their values in Column-II, but in a different order. Match them. Gravitational field is measured in units of \((GM/R^2),\) potential in units of \(\left(-\dfrac{GM}{R}\right)\) while potential energy is in units of \((-GM^2/R)\)
| Column-I | Column-II | ||
| \(\mathrm{(A)}\) | Gravitational potential energy (PE) of interaction between the sphere and the ring. | \(\mathrm{(I)}\) | \(1.25\) |
| \(\mathrm{(B)}\) | Gravitational potential at the common centre \((O)\) | \(\mathrm{(II)}\) | \(1.36\) |
| \(\mathrm{(C)}\) | Gravitational potential at \(P,\) a pole of the sphere. | \(\mathrm{(III)}\) | \(2\) |
| \(\mathrm{(D)}\) | Gravitational field at \(P,\) a pole of the sphere. | \(\mathrm{(IV)}\) | \(2.75\) |
| 1. | \(\mathrm{A\text-I,B\text-IV,C\text-III,D\text-II}\) |
| 2. | \(\mathrm{A\text-II,B\text-III,C\text-I,D\text-IV}\) |
| 3. | \(\mathrm{A\text-III,B\text-II,C\text-IV,D\text-I}\) |
| 4. | \(\mathrm{A\text-I,B\text-IV,C\text-II,D\text-III}\) |
Subtopic: Gravitational Potential |
To view explanation, please take trial in the course below.
NEET 2026 - Target Batch - Vital
To view explanation, please take trial in the course below.
NEET 2026 - Target Batch - Vital
Please attempt this question first.
Launched MCQ Practice Books
Prefer Books for Question Practice? Get NEETprep's Unique MCQ Books with Online Audio/Video/Text Solutions via Telegram Bot
NEET MCQ Books for XIth & XIIth Physics, Chemistry & Biology- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.