Ncert Exercises & Solutions

The displacement of a particle moving along a straight line is given by:
$x = (t-2)^2,$
where $t$ is in seconds. What is the total distance travelled by the particle in the first $4~\text{s}?$
1. $4~\text{m}$
2. $8~\text{m}$
3. $12~\text{m}$
4. $16~\text{m}$

(b) Hint: Area of v-t graph without signs gives the distance.

Step 1: Find the velocity and acceleration of the particle.

$\begin{array}{ll} Given, & x = (t - 2)^{2} \\ Velocity, & v = \frac{dx}{dt} = \frac{d}{dt} (t - 2)^{2} = 2 (t - 2) m / s \\ Acceleration, & a = \frac{dv}{dt} = \frac{d}{dt} [2 (t - 2)] \\ = 2 [1 - 0] = 2 m / s^{2} \\ When, & t = 0; v = - 4 m / s \\ t = 2 s; v = 0 m / s \\ t = 4 s; v = 4 m / s \end{array}$

Step 2: Draw v-t graph.

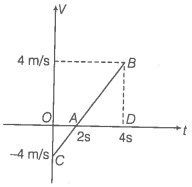
v - t graph is shown in the adjacent diagram.

Step 3: Find the distance covered by the particle.
Distance traveled = area of the graph

$\begin{array}{l} = area OAC + area ABD \\ = \frac{4 \times 2}{2} + \frac{1}{2} \times 2 \times 4 = 8 m \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions