Ncert Exercises & Solutions

A three-wheeler starts from rest and accelerates uniformly at $1~\text{m/s}^2$ on a straight road for $10~\text s,$ then moves with uniform velocity. If $s_n$ is the distance covered during the $n^{th}$ second $(n=1,2,3,....),$ what will the plot of $s_n$ vs $n$ look like during the accelerated motion?
1. A horizontal line (constant)
2. A straight line (linear)
3. A parabola (quadratic)
4. An exponential curve

Distance covered by a body in nth second is given by the relation

$D = u + \frac{a}{2} (2 n - 1) . . . (i)$

Where,

u = Initial velocity

a = Acceleration

n = Time = 1, 2, 3, ..... , n

In the given case, u = 0 and a = $1 m / s^{2}$

$\Rightarrow D_{n} = \frac{1}{2} (2 n - 1) . . . (i i)$
$O r, D_{n} \propto n . . . (i i i)$ Now, substituting different values of n in equation (iii), we get the following table:

0.5

1.5

2.5

3.5

4.5

5.5

6.5

7.5

8.5

9.5

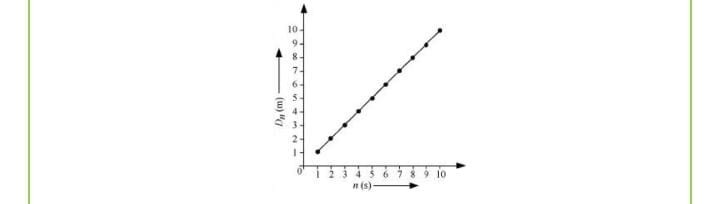
$T h e r e f o r e, t h e g r a p h b e t w e e n n a n d D_{n} w i l l b e s t r a i g h t l i n e$

Since the given three-wheeler acquires uniform velocity after 10 s, the line will be parallel to the time-axis after n = 10 s.

3.24 A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m s–1. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m s-1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?

The initial velocity of the ball, u = 49 m/s
Acceleration, a = – g = – 9.8 m/s²

Case I:
When the lift was stationary, the boy throws the ball.
Taking upward motion of the ball,
Final velocity, v of the ball becomes zero at the highest point.
From the first equation of motion, time of ascent (t) is given as:
v = u +at

\frac{- 49}{- 9.8} = 5 s .

\Rightarrow t = \frac{(v - u)}{a}

But, the time of ascent is equal to the time of descent.
Hence, the total time taken by the ball to return to the boy’s hand = 5 + 5 = 10 s.
Case II:
The lift was moving up with a uniform velocity of 5 m/s. In this case, the relative velocity of the ball with respect to the boy remains the same i.e., 49 m/s. Therefore, in this case, also, the ball will return back to the boy’s hand after 10 s.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions