Ncert Exercises & Solutions

Q. 29 Two identical heavy spheres are separated by a distance of 10 times their radius. Will an object placed at the mid-point of the line joining their centres be in a stable equilibrium or unstable equilibrium? Give a reason for your answer.

Hint: In stable equilibrium, the forces acting on the body try to bring the body in the original position when the body is slightly displaced.

Step 1: Find the net force on the object.

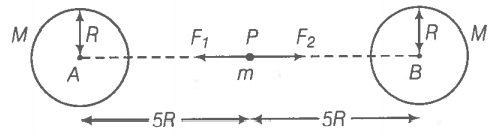
Let the mass and radius of each identical heavy sphere be M and R respectively. An object of mass m is placed at the mid-point P of the line joining their centres.

Force acting on the object placed at the mid-point,

F_{1} = F_{2} = \frac{G M m}{{(5 R)}^{2}}

The direction of forces are opposite, therefore the net force acting on the object is zero.

Step 2: Find the net force on the object again when the object is displaced.

To check the stability of the equilibrium, we displace the object through a small distance x towards sphere A.

Now, the force acting towards sphere A,

F'_{1} = \frac{G M m}{{(5 R - x)}^{2}}

Force acting towards sphere B,

F_{2}' = \frac{G M m}{{(5 R + x)}^{2}}

F_{1}' > F_{2}',

therefore a resultant force

(F_{1}' - F_{2}')

acts on the object towards sphere A, therefore the object starts to move towards sphere A and hence equilibrium is unstable.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions