Ncert Exercises & Solutions

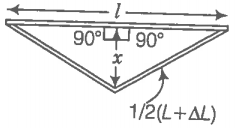
A rail track made of steel having a length of 10 m is clamped on a railway line at its two ends (figure). On a summer day, due to a rise in temperature by 20° C, it is deformed as shown in the figure. Find x (displacement of the centre) if $α_{s t e e l} = 1.2 \times 10^{- 5} / ° C .$

Hint: The shape of the rail changes due to the thermal expansion of the rail.

Consider the diagram.

Step 1: Find the value of x in terms of L and

∆

L .

Applying Pythagoras theorem in the right-angled triangle in the figure.

{(\frac{L + ∆ L}{2})}^{2} = {(\frac{L}{2})}^{2} + x^{2}

\Rightarrow x = \sqrt{{(\frac{L + ∆ L}{2})}^{2} - {(\frac{L}{2})}^{2}}

= \frac{1}{2} \sqrt{{(L + ∆ L)}^{2} - L^{2}}

= \frac{1}{2} \sqrt{(L^{2} + ∆ L^{2} + 2 L ∆ L) - L^{2}}

= \frac{1}{2} \sqrt{(∆ L^{2} + 2 L ∆ L)}

An increase in length

∆

L is very small, therefore, neglecting

{(∆ L)}^{2}

, we get,

x = \frac{1}{2} \times \sqrt{2 L ∆ L}

...(i)

But,

∆ L = L α ∆ t

...(ii)

Step 2: Put the numerical values of L and

∆

Substituting the value of

∆ L

in Eq. (i) from Eq. (ii):

x = \frac{1}{2} \sqrt{2 L \times L α ∆ t} = \frac{1}{2} L \sqrt{2 α ∆ t}

= \frac{10}{2} \times \sqrt{2 \times 1.2 \times 10^{- 5} \times 20}

= 5 \times \sqrt{4 \times 1.2 \times 10^{- 4}}

= 5 \times 2 \times 1.1 \times 10^{- 2} = 0.11 m = 11 c m

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions