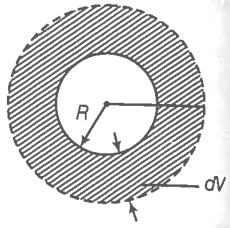
The radius of a metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is . The sphere heated a little by a temperature T so that its new temperature is T+T. The increase in the volume of the sphere is approximately:
1.
2.
3.
4.

© 2026 GoodEd Technologies Pvt. Ltd.