Ncert Exercises & Solutions

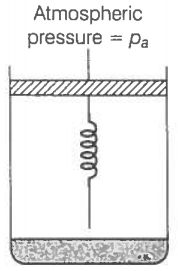
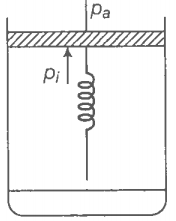
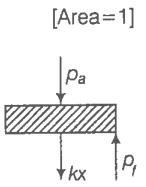
Consider one mole of a perfect gas in a cylinder of the unit cross-section with
a piston attached (figure). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially, the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of value from $V_{o}$ $V_{o}$ to $V_{1}$ $V_{1}$ .
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down the relation between Q, $P_{a}$ $P_{a}$ , $V_{1}$ $V_{1}$ , $V_{o}$ $V_{o}$ and k.

Hint: The work is done by the gas against the atmospheric pressure and the spring force.

a) Step 1: Find the initial pressure.

Initially, the piston is in equilibrium hence,

P_{i} = P_{a}

$P_{i} = P_{a}$

(b) Step 2: Find the final pressure.

On supplying heat, the gas expands from

V_{0} t o V_{1}

$V_{0} t o V_{1}$ .

∴

$∴$ Increase in volume of the gas

= V_{1} - V_{0}

$= V_{1} - V_{0}$

As the piston has the unit cross-sectional area, hence, the extension in the spring:

x = \frac{V_{1} - V_{0}}{A r e a} = V_{1} - V_{0}

$x = \frac{V_{1} - V_{0}}{A r e a} = V_{1} - V_{0}$

∴

$∴$ Force exerted by the spring on the piston

= F = k x = k (V_{1} - V_{0})

$= F = k x = k (V_{1} - V_{0})$

Hence, the final pressure,

P_{f} = P_{a} + k x

$P_{f} = P_{a} + k x$

= P_{a} + k \times (V_{1} - V_{0})

$= P_{a} + k \times (V_{1} - V_{0})$

From first law of thermodynamics, dQ= dU+ dW

If T is the final temperature of the gas, then the increase in internal energy,

d U = C_{V} (T - T_{0}) = C_{V} (T - T_{0})

$d U = C_{V} (T - T_{0}) = C_{V} (T - T_{0})$

We can write,

T = \frac{P_{f} V_{1}}{R} = [\frac{P_{a} + k (V_{1} - V_{0})}{R}] \frac{V_{1}}{R}

$T = \frac{P_{f} V_{1}}{R} = [\frac{P_{a} + k (V_{1} - V_{0})}{R}] \frac{V_{1}}{R}$

Work done by the gas =

P_{a}

$P_{a}$

Δ

$∆$ V + increase in PE of the spring

= P_{a} (V_{1} - V_{0}) + \frac{1}{2} k x^{2}

$= P_{a} (V_{1} - V_{0}) + \frac{1}{2} k x^{2}$

Now, we can write, dQ = dU+dW

$= C_{V} (T - T_{0}) + P_{a} (V_{1} - V_{0}) + \frac{1}{2} k x^{2}$

$= C_{V} (T - T_{0}) + P_{a} (V_{1} - V_{0}) + \frac{1}{2} k {(V_{1} - V_{0})}^{2}$ ₁-V₀)2

This is the required relation.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions