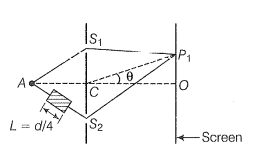
Hint: The position of the maxima or minima depends on the path difference.

Step 1: Find the path difference.

ln case of transparent glass slab of refractive index, the path difference will be calculated 

as $∆\mathrm{x}=2\mathrm{d}<mspace\; width="1em"></mspace>\mathrm{sin\theta }<mspace\; width="1em"></mspace>+(\mathrm{\mu }-1)\mathrm{L}$

Step 2: Find the condition for maxima.

For the principal maxima, the path difference= 0 

$2\mathrm{d}<mspace\; width="1em"></mspace>\mathrm{sin\theta }<mspace\; width="1em"></mspace>+(\mathrm{\mu }-1)\mathrm{L}=0$
$\mathrm{or}<mspace\; width="1em"></mspace><mspace\; width="1em"></mspace><mspace\; width="1em"></mspace>{\mathrm{sin\theta }}_0<mspace\; width="1em"></mspace>=<mspace\; width="1em"></mspace>-\frac{\mathrm{L}(\mathrm{\mu }-1)}{2\mathrm{d}}<mspace\; width="1em"></mspace>=\frac{-\mathrm{L}(0.5)}{2\mathrm{d}}<mspace\; width="1em"></mspace><mspace\; width="1em"></mspace><mspace\; width="1em"></mspace><mspace\; width="1em"></mspace><mspace\; width="1em"></mspace><mspace\; width="1em"></mspace>\left[\therefore \mathrm{L}<mspace\; width="1em"></mspace>=\mathrm{d}/4\right]$
$\mathrm{or}<mspace\; width="1em"></mspace>\sin <mspace\; width="1em"></mspace>{\mathrm{\theta }}_0=\frac{-1}{16}$
$\mathrm{OP}=\mathrm{D}<mspace\; width="1em"></mspace>\tan <mspace\; width="1em"></mspace>{\mathrm{\theta }}_0=\mathrm{D}<mspace\; width="1em"></mspace>\sin <mspace\; width="1em"></mspace>{\mathrm{\theta }}_0=\frac{-\mathrm{D}}{16}$

Step 2: Find the condition for minima.

For the first minima, the path difference is $\pm \frac{\mathrm{\lambda }}{2}$.

$\begin{array}{rl}2\mathrm{dsin}{\mathrm{\theta }}_1+0.5\mathrm{L}& =\pm \frac{\mathrm{\lambda }}{2}\\ \sin {\mathrm{\theta }}_1& =\frac{\pm \mathrm{\lambda }/2-0.5\mathrm{L}}{2\mathrm{d}}=\frac{\pm \mathrm{\lambda }/2-\mathrm{d}/8}{2\mathrm{d}}\\ & =\frac{\pm \mathrm{\lambda }/2-\mathrm{\lambda }/8}{2\mathrm{\lambda }}=\pm \frac{1}{4}-\frac{1}{16}\end{array}$

[ The diffraction occurs if the wavelength of waves is nearly equal to the slit width (d)] 

On the positive side, sin${{\theta }_1}^{+}=\frac{1}{4}-\frac{1}{16}=\frac{3}{16}$

On the negative side, sin ${{\theta }_1}^{-}=\frac{1}{4}-\frac{1}{16}=-\frac{5}{16}$

The first principal maxima on the positive side is at distance:

$\tan {\theta }_1^{\mathrm{\prime }+}=D\frac{\sin {\theta }_1^{\mathrm{\prime }+}}{\sqrt{1-{\sin }^2{\theta }_1^{\mathrm{\prime }}}}=D\frac{3}{\sqrt{{16}^2-3^2}}=\frac{3D}{\sqrt{247}}<mspace\; width="1em"></mspace>\text{above point\hspace{0.17em}}O$

The first principal minima on the negative side is at distance 

D tan ${{\mathrm{\theta }}_1}^{+}=\frac{5\mathrm{D}}{\sqrt{{16}^2-5^2}}=\frac{5\mathrm{D}}{\sqrt{231}}<mspace\; width="1em"></mspace>\mathrm{below}<mspace\; width="1em"></mspace>\mathrm{point}<mspace\; width="1em"></mspace>\mathrm{O}.$