Ncert Exercises & Solutions

Show that for a material with refractive index μ ≥ $\sqrt2$, light incident at any angle shall be guided along a length perpendicular to the incident face.

Hint: The refraction of light depends on the refractive index of the material.

Step 1: Find the angle of refraction at the first surface.

Any ray entering at an angle i shall be guided along AC if the angle ray makes with a face AC $(ϕ)$ is greater than the critical angle as per the principle of total internal reflection.

So, $ϕ + r = 90 °$ , therefore, sin $ϕ$ = cos r

$\Rightarrow \sin ϕ \geq \frac{1}{μ}$
$\Rightarrow \cos r \geq \frac{1}{μ}$
$or 1 - \cos^{2} r \leq 1 - \frac{1}{μ^{2}}$
$i . e ., \sin^{2} r \leq 1 - \frac{1}{μ^{2}}$
$Step 2 : Find the angle of incidence .$
$Since, \sin i = μ sinr$
$\frac{1}{μ^{2}} \sin^{2} i \leq 1 - \frac{1}{μ^{2}} or \sin^{2} i \leq μ^{2} - 1$
$When i = \frac{π}{2}, we have the smallest angle ϕ .$

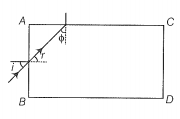
Step 3: Find the refractive index of the material.
If that is greater than the critical angle, then all other angles of incidence shall be more than the critical angle.
Thus, $1 \leq μ^{2} - 1$
or $μ^{2} \geq 2$
$\Rightarrow μ \geq \sqrt{2}$
This is the required result.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions