Hint: The net current will be equal to the sum of currents flowing in the two branches.
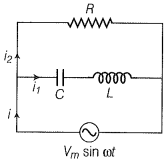
Step 1: In the given figure i is the total current from the source. It is divided into two parts through R and through series combination of C and L.
So, we can write; i=+
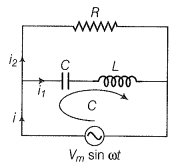
Step 2: If is the charge on the capacitor at any time t, then for a series combination of C and L, applying KVL in the lower Circuit as shown;
Step 3: Now putting these values in Eq. (ii), we get;
Step 4: From Eqs. (i) and (v), we find that are out of phase by .
This is the expression for impedance Z of the circuit.