Ncert Exercises & Solutions

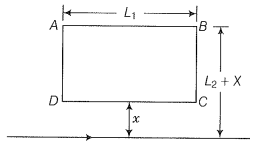
A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current $I (t) = I_{0} (1 - t / T) for 0 \leq t \leq T$ and I(0)=0 for t>T (figure). Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.

Hint: The change in current results in a change in magnetic field through the loop.

The emf induced can be obtained b differentiating the expression of magnetic flux linked wrt t nad then applying Ohm's law

Step 1 : I = \frac{ε}{R} = \frac{1}{R} \frac{dφ}{dt}

We know that electric current;

I (t) = \frac{dQ}{dt} or \frac{dQ}{dt} = \frac{1}{R} \frac{dφ}{dt}

Step 2 : Integrating the variables separately in the form of a differential equation for finding the charge

Q that passed in time t, we have;

Q (t_{1}) - Q (t_{2}) = \frac{1}{R} [ϕ (t_{1}) - ϕ (t_{2})]

ϕ (t_{1}) = L_{1} \frac{μ_{0}}{2 π} \int_{x}^{L_{2} + x} \frac{dx'}{x'} I (t_{1})

= \frac{μ_{0} L_{1}}{2 π} I (t_{1}) \ln (\frac{L_{2} + x}{x})

Step 3 : The magnitude of charge is given by,

= \frac{μ_{0} L_{1}}{2 π} In \frac{L_{2} + x}{x} [I_{0} + 0]

= \frac{μ_{0} L_{1}}{2 π} I_{1} \times In (\frac{L_{2} + x}{x})

This is the required expression .

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions