A conducting wire XY of mass m and negligible resistance slides smoothly on two parallel conducting wires as shown in the figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field B=B(t).
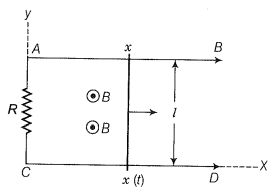
(i) Write down the equation for the acceleration of the wire XY.
(ii) If B is independent of time, obtain v(t), assuming v(0)=
(iii) For (ii), showing that the decrease in kinetic energy of XY equals the heat lost in.

© 2026 GoodEd Technologies Pvt. Ltd.