Ncert Exercises & Solutions

Question 2.22:

Figure 2.34 shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).

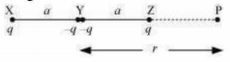
Four charges of the same magnitude are placed at points X, Y, Y, and Z respectively, as shown in the following figure.

A point is located at P, which is r distance away from Y.

The system of charges forms an electric quadrupole.

It can be considered that the system of electric quadrupole has three charges. Charge +q placed at point X

Charge —2q placed at point Y

Charge +q placed at point Z

XY = YZ = a

YP - r

PX = r + a

PZ = r - a

Electrostatic potential caused by the system of three charges at point P is given by,

$\begin{aligned} V & = \frac{1}{4 {πϵ}_{0}} [\frac{q}{XP} - \frac{2 q}{YP} + \frac{q}{ZP}] \\ = \frac{1}{4 {πϵ}_{0}} [\frac{q}{r + a} - \frac{2 q}{r} + \frac{q}{r - a}] \\ = \frac{q}{4 {πϵ}_{0}} [\frac{r (r - a) - 2 (r + a) (r - a) + r (r + a)}{r (r + a) (r - a)}] \\ = \frac{q}{4 {πϵ}_{0}} [\frac{r^{2} - ra - 2 r^{2} + 2 a^{2} + r^{2} + ra]}{r (r^{2} - a^{2})}] = \frac{q}{4 {πϵ}_{0}} [\frac{2 a^{2}}{r (r^{2} - a^{2})]} \\ = \frac{2 {qa}^{2}}{4 {πϵ}_{0} r^{3} (1 - \frac{a^{2}}{r^{2}})} \end{aligned}$

$\begin{aligned} since \frac{r}{a} >> 1 \\ ∴ \frac{a}{r} << 1 \\ \frac{a^{2}}{r^{2}} is taken as negligible. \\ ∴ V = \frac{2 {qa}^{2}}{4 {πϵ}_{0} r^{3}} \end{aligned}$

It can be inferred that potential,

$V \propto \frac{1}{r^{3}}$

However, it is known that for a dipole,

$V \propto \frac{1}{r^{2}}$

And, for a monopole,

$V \propto \frac{1}{r}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions