A cube of side \(b\) has a charge \(q\) at each of its vertices. Determine the potential \(V\) and the magnitude of the electric field \(E\) due to this charge array at the center of the cube.
1. \(V=\dfrac{4q}{\sqrt 3 \pi \epsilon_0 b},~E=0\)
2. \(V=\dfrac{2q}{\sqrt 3 \pi \epsilon_0 b},~E=0\)
3. \(V=\dfrac{4q}{\sqrt 3 \pi \epsilon_0 b},~E=\dfrac{q}{4 \pi \epsilon_0 b^2}\)
4. \(V=\dfrac{q}{ \pi \epsilon_0 b},~E=\dfrac{q}{4 \sqrt 3\pi \epsilon_0 b^2}\)
Length of the side of a cube = b
Charge at each of its vertices = q
A cube of side b is shown in the following figure.
d Diagonal of one of the six faces of the cube
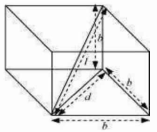
I= Length of the diagonal of the cube
is the distance between the center of the cube and one of the eight vertices
The electric potential (V) at the center of the cube is due to the presence of eight charges at the vertices.
Therefore, the potential at the center of the cube is .
The electric field at the center of the cube, due to the eight charges, gets canceled. This is because the charges are distributed symmetrically with respect to the center of the cube. Hence, the electric field is zero at the center.

© 2026 GoodEd Technologies Pvt. Ltd.