Ncert Exercises & Solutions

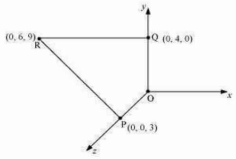
A charge of $8~\text{mC}$ is located at the origin. Calculate the work done in taking a small charge of $-2 \times 10^{-9}~\text C$ from a point $P(0, 0, 3~\text{cm})$ to a point $Q(0,~4~\text{cm},~0),$ via a point $R(0,~6~\text{cm},~9~\text{cm}).$
1. $0~\text J$
2. $1.2~\text J$
3. $2.4~\text J$
4. $9.6~\text J$

Charge located at the origin, q = 8 8 x 10-3 C

The magnitude of a small charge, which is taken from a point P to point R to point - 2 x 10-9C

All the points are represented in the given figure.

Point P is at a distance, dl = 3 cm, from the origin along the z-axis.

Point Q is at a distance, dz = 4 cm, from the origin along the y-axis.

potential at point p, $V_{1} = \frac{q}{4 π ϵ_{0} \times d_{1}}$

The potential at point Q, $V_{2} = \frac{q}{4 π ϵ_{0} d_{2}}$

Work done (W) by the electrostatic force is independent Of the path.

$\begin{array}{l} ∴ W = q_{1} [V_{2} - V_{1}] \\ = q_{1} [\frac{q}{4 π ϵ_{0} d_{2}} - \frac{q}{4 π ϵ_{0} d_{1}}] \\ = \frac{q q_{1}}{4 π ϵ_{0} [\frac{1}{d_{2}} - \frac{1}{d_{1}}]} \\ Where, \frac{1}{4 π ϵ_{0}} = 9 \times 10^{\circ} N m^{2} C^{- 2} \\ ∴ W = 9 \times 10^{9} \times 8 \times 10^{- 3} \times (- 2 \times 10^{- 9}) [\frac{1}{0.04} - \frac{1}{0.03}] \\ = - 144 \times 10^{- 3} \times (\frac{- 25}{3}) \\ = 1.27 J \end{array}$

Therefore, the work done during the process is 1.27 J.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions