Q. 23 Find the center of mass of a uniform (a) half-disc, (b) quarter-disc.
Let M and R be the mass and radius of the half-disc, mass per unit area of the half-disc
Step 2: Find the position of center of mass of small element.
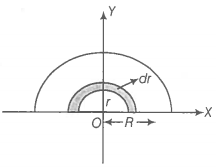
(a) The half-disc can be supposed to be consists of a large number of semicircular rings of mass dm and thickness d, and radii ranging from r = 0 to r = R.
The surface area of semicircular ring of radius r and of thickness
Mass of this elementary ring,
If (x, y) are coordinates of the center of mass of this element, then,
Let be the coordinates of the center of mass of the semicircular disc.
Then
Step 3: Find the position of center of mass for half-disc.
(b)
Step 4: Find centre of mass of a uniform quarter disc.
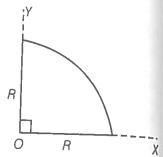
using symmetry
For a half-disc along the y-axis center of mass be at
For a half-disc along the x-axis center of mass will be at
Hence, for the quarter disc center of mass

© 2026 GoodEd Technologies Pvt. Ltd.