4.34. A river is flowing due east with a speed 3 m/s. A swimmer can swim in still water at a speed of 4 m/s.
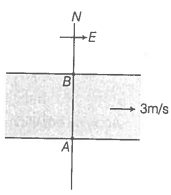
a) if swimmer starts swimming due north, what will be his resultant velocity?
b) if he wants to start from point A on south bank and reach opposite point B on north bank,
i) which direction should he swim?
ii) what will be his resultant speed?
c) from two different cases as mentioned in a) and b) above, in which case will he reach opposite bank in shorter time?
Given, Speed of the river () = 3m/s (east)
Speed of swimmer () = 4 m/s (east)
a) When the swimmer starts swimming due north then his resultant velocity
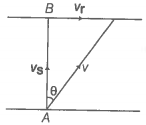
Step 2: Find the velocity of the swimmer so that he reaches directly opposite point.
(b) To reach opposite points B, the swimmer should swim at an angle of the north. Resultant speed of the swimmer
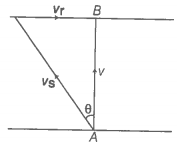
Step 3: Calculate the shortest time taken by the swimmer.
(c) In case (a).
Time is taken by the swimmer to cross the river,
In case (b).
Time is taken by the swimmer to cross the river
Hence, the swimmer will cross the river in a shorter time in case (a).

© 2026 GoodEd Technologies Pvt. Ltd.