Please be patient as the PDF generation may take upto a minute.

When a rubber-band is stretched by a distance x, it exerts a restoring force of magnitude $\mathrm{F}=\mathrm{ax}+{\mathrm{bx}}^2$ where a and b are constants. The work done in stretching the unstretched rubber-band by L is 
1. ${\mathrm{aL}}^2+{\mathrm{bL}}^3$
2. $\frac{1}{2}\left({\mathrm{aL}}^2+{\mathrm{bL}}^3\right)$
3. $\frac{{\mathrm{aL}}^2}{2}+\frac{{\mathrm{bL}}^3}{3}$
4. $\frac{1}{2}\left(\frac{{\mathrm{aL}}^2}{2}+\frac{{\mathrm{bL}}^3}{3}\right)$

The work done on a particle of mass m by a force $\mathrm{K}\left[\frac{\mathrm{x}}{{\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)}^{3/2}}\hat{\mathrm{i}}+\frac{\mathrm{y}}{{\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)}^{3/2}}\hat{\mathrm{j}}\right]$ ( K being a constant of appropriate dimensions), when the particle is taken from the point (a,0) to the point (0,a) along a circular path of radius a about the origin in the x-y plane is 
1. $\frac{2\mathrm{K\pi }}{\mathrm{a}}$
2. $\frac{\mathrm{K\pi }}{\mathrm{a}}$
3. $\frac{\mathrm{K\pi }}{2\mathrm{a}}$
4. 0

The potential energy function for the force between two atoms in a diatomic molecule is approximately given by  $\mathrm{U}\left(\mathrm{x}\right)=\frac{\mathrm{a}}{{\mathrm{x}}^{12}}-\frac{\mathrm{b}}{{\mathrm{x}}^6}$, where a and b are constants and x is the distance atoms. If the dissociation energy of the molecule is $\mathrm{D}=\left[\mathrm{U}\left(\mathrm{x}=\infty \right)-{\mathrm{U}}_{\mathrm{at} \mathrm{equilibrium}}\right]$, D is
1. $\frac{{\mathrm{b}}^2}{6\mathrm{a}}$
2. $\frac{{\mathrm{b}}^2}{2\mathrm{a}}$
3. $\frac{{\mathrm{b}}^2}{12\mathrm{a}}$
4. $\frac{{\mathrm{b}}^2}{4\mathrm{a}}$

A particle in a certain conservative force field has a potential energy given by U = $\frac{20\mathrm{xy}}{\mathrm{z}}$. The force exerted on it is
$1. \left(\frac{20\mathrm{y}}{\mathrm{z}}\right)\hat{\mathrm{i}}+ \left(\frac{20\mathrm{x}}{\mathrm{z}}\right)\hat{\mathrm{j}}+ \left(\frac{20\mathrm{xy}}{{\mathrm{z}}^2}\right)\hat{\mathrm{k}}$
$$
$2. -\left(\frac{20\mathrm{y}}{\mathrm{z}}\right)\hat{\mathrm{i}}- \left(\frac{20\mathrm{x}}{\mathrm{z}}\right)\hat{\mathrm{j}}+ \left(\frac{20\mathrm{xy}}{{\mathrm{z}}^2}\right)\hat{\mathrm{k}}$
$$
$3. -\left(\frac{20\mathrm{y}}{\mathrm{z}}\right)\hat{\mathrm{i}}- \left(\frac{20\mathrm{x}}{\mathrm{z}}\right)\hat{\mathrm{j}}- \left(\frac{20\mathrm{xy}}{{\mathrm{z}}^2}\right)\hat{\mathrm{k}}$
$$
$4. \left(\frac{20\mathrm{y}}{\mathrm{z}}\right)\hat{\mathrm{i}}+ \left(\frac{20\mathrm{x}}{\mathrm{z}}\right)\hat{\mathrm{j}}- \left(\frac{20\mathrm{xy}}{{\mathrm{z}}^2}\right)\hat{\mathrm{k}}$

A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
$1. {\mathrm{t}}^{1/2}$
$2. \mathrm{t}$
$3. {\mathrm{t}}^{3/2}$
$4. {\mathrm{t}}^2$

Two particles \(A\) and \(B,\) move with constant velocities \(\vec{v_1}\) and \(\vec{v_2}.\) At the initial moment their position vector are \(\vec {r_1}\) and \(\vec {r_2}\) respectively. The conditions for particles \(A\) and \(B\) for their collision to happen will be:

A particle of mass 'm' is moving in circular path of constant radius 'r' such that centripetal acceleration is varying with time 't' as ${\mathrm{K}}^2{\mathrm{rt}}^2$ where K is a constant. The power delivered to the particle by the force acting on it is
$1. {\mathrm{m}}^2{\mathrm{K}}^2{\mathrm{r}}^2{\mathrm{t}}^2$
$2. {\mathrm{mK}}^2{\mathrm{r}}^2\mathrm{t}$
$3. {\mathrm{mK}}^2{\mathrm{rt}}^2$
$4. {\mathrm{mKr}}^2\mathrm{t}$

A particle falls from a height h upon a fixed horizontal plane and rebounds. If e is the coefficient of restitution, the total distance travelled before rebounding has stopped is
1. \(h\left ( \frac{1+e^{2}}{1-e^{2}} \right )\)
2. \(h\left ( \frac{1-e^{2}}{1+e^{2}} \right )\)
3. \(\frac{h}{2}\left ( \frac{1-e^{2}}{1+e^{2}} \right )\)
4. \(\frac{h}{2}\left ( \frac{1+e^{2}}{1-e^{2}} \right )\)

If ${\mathrm{W}}_1, {\mathrm{W}}_2$ and ${\mathrm{W}}_3$ represent the work done in moving a particle from A to B along three different paths 1, 2 and 3 respectively (as shown) in the gravitational field of a point mass m, find the correct relation between ${\mathrm{W}}_1, {\mathrm{W}}_2$ and ${\mathrm{W}}_3$.

$1. {\mathrm{W}}_1>{\mathrm{W}}_2>{\mathrm{W}}_3$
$2. {\mathrm{W}}_1= {\mathrm{W}}_2= {\mathrm{W}}_3$
$3. {\mathrm{W}}_1<{\mathrm{W}}_2<{\mathrm{W}}_3$
$4. {\mathrm{W}}_2>{\mathrm{W}}_1>{\mathrm{W}}_3$

Consider elastic collision of a particle of a mass m moving with a velocity u with another particle of the same mass at rest. After the collision the projectile and the struck particle move in directions making angle ${\mathrm{\theta }}_1$ and ${\mathrm{\theta }}_2$ respectively with the initial direction of motion. The sum of the angles. ${\mathrm{\theta }}_1+ {\mathrm{\theta }}_2$, is
$1. {45}^{\mathrm{o}}$
$2. {90}^{\mathrm{o}}$
$3. {135}^{\mathrm{o}}$
$4. {180}^{\mathrm{o}}$

Two small particles of equal masses moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are v and 2v, respectively, as shown in the figure. Between collisions, the particles move with constant speed. After making how many elastic collisions, other than that at A, these two particles will again reach the point A

1. 4
2. 3
3. 2
4. 1

A cord is used to lower vertically a block of mass M by a distance d with constant downward acceleration $\frac{\mathrm{g}}{4}$. Work done by the cord on the block is
$1. \mathrm{Mg}\frac{\mathrm{d}}{4}$
$2. 3\mathrm{Mg}\frac{\mathrm{d}}{4}$
$3. -3\mathrm{Mg}\frac{\mathrm{d}}{4}$
$4. \mathrm{Mgd}$

A frictionless track ABCDE ends in a circular loop of radius R. A body slides down from point A which is at a height h = 5 cm. Maximum value of R for the body to successfully complete the loop is

$1. 5 \mathrm{cm}$
$2. \frac{15}{4} \mathrm{cm}$
$3. \frac{10}{3} \mathrm{cm}$
$4. 2 \mathrm{cm}$
 

A body is moved along a straight line by a machine delievering constant power. The distance moved by the body in time t is proportional to 
1. t^1/2
2. t^3/4
3. t^3/2
4. t²

A particle is moving in a circle of radius r under the action of a force F = ${\mathrm{ar}}^2$ which is directed towards centre of the circle. Total mechanical energy (kinetic energy + potential energy) of the particle is (take potential energy = 0 for r = 0)
$1. \frac{1}{2}{\mathrm{\alpha r}}^3$
$2. \frac{5}{6}{\mathrm{\alpha r}}^3$
$3. \frac{4}{3}{\mathrm{\alpha r}}^3$
$4. {\mathrm{\alpha r}}^3$

A particle is moving in a circular path of radius a under the action of an attractive potential U = $-\frac{\mathrm{k}}{2{\mathrm{r}}^2}$. Its total energy is:
$1. -\frac{\mathrm{k}}{4{\mathrm{a}}^2}$
$2. \frac{\mathrm{k}}{2{\mathrm{a}}^2}$
$3. \mathrm{zero}$
$4. -\frac{3}{2}\frac{\mathrm{k}}{{\mathrm{a}}^2}$

A stone is tied to a string of length $\mathcal{l}$ and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
$1. \sqrt{2\mathrm{g}\mathcal{l}}$
$2. \sqrt{2({\mathrm{u}}^2- \mathrm{g}\mathcal{l})}$
$3. \sqrt{{\mathrm{u}}^2- \mathrm{g}\mathcal{l}}$
$4. \mathrm{u}- \sqrt{{\mathrm{u}}^2- 2\mathrm{g}\mathcal{l}}$

Consider a drop of rain water having mass 1 g falling from a height of 1 km. It hits the ground with a speed of 50 m/s. Take 'g' constant with a value 10 $\mathrm{m}/{\mathrm{s}}^2$. The work done by the (i) gravitational force and the (ii) resistive force of air
1. (i) 1.25 J (ii) -8.25 J
2. (i) 100 J (ii) 8.75 J
3. (i) 10 J (ii) -8.75 J
4. (i) -10 J (ii) -8.25 J

Consider a drop of rain water having mass 1 g falling from a height of 1 km. It hits the ground with a speed of 50 m/s. Take 'g' constant with a value 10 $\mathrm{m}/{\mathrm{s}}^2$. The work done by the (i) gravitational force and the (ii) resistive force of air
1. (i) 1.25 J (ii) -8.25 J
2. (i) 100 J (ii) 8.75 J
3. (i) 10 J (ii) -8.75 J
4. (i) -10 J (ii) -8.25 J

A body of mass m = ${10}^{-2}$ kg is moving in a medium and experiences a frictional force F = $-{\mathrm{kv}}^2$. Its initial speed is ${\mathrm{v}}_0$ = 10 ${\mathrm{ms}}^{-1}$. If, after 10 s, its energy is $\frac{1}{8}{\mathrm{mv}}_0^2$, the value of k will be:
$1. {10}^{-4} \mathrm{kg} {\mathrm{m}}^{-1}$
$2. {10}^{-1} \mathrm{kg} {\mathrm{m}}^{-1} {\mathrm{s}}^{-1}$
$3. {10}^{-3} \mathrm{kg} {\mathrm{m}}^{-1}$
$4. {10}^{-3} \mathrm{kg} {\mathrm{s}}^{-1}$

Figure shows a bob of mass m suspended from a string of length L. The velocity is ${\mathrm{V}}_0$ at A, then the potential energy of the system is ________ at the lowest point A.

$1. \frac{1}{2}{\mathrm{m}}_0^2$
$2. \mathrm{mgh}$
$3. \frac{-1}{2}{\mathrm{mv}}_0^2$
$4. \mathrm{zero}$

The given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them, r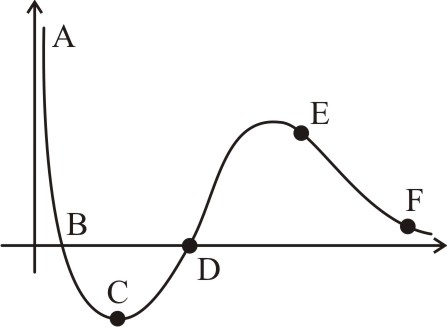

1. B and D are equilibrium points
2. C is a point of stable equlibrium
3. The force of interaction between the two particles is attractive between points C and D and repulsive between points D and E on the curve.
4. The force of interaction between the particles is attractive between points E and F on the curve.