Please be patient as the PDF generation may take upto a minute.

A ball is dropped vertically from a height \(h\) above the ground. It hits the ground and bounces up vertically to a height of \(\frac{h}{2}\). Neglecting subsequent motion and air resistance, its velocity \(v\) varies with the height \(h\) as:
[Take vertically upwards direction as positive.]

1.		2.
3.		4.

The graph of displacement time is given below.
 
Its corresponding velocity-time graph will be:

1.		2.
3.		4.

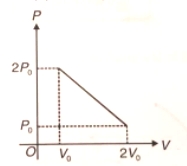
1. \(2P_0 - \frac{P_0V}{V_0}\)
2. \(3P_0 - \frac{P_0V}{V_0}\)
3. \(P_0 - \frac{P_0V}{V_0}\)
4. \(4P_0 - \frac{P_0V}{V_0}\)

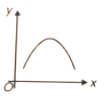
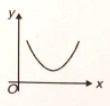
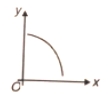
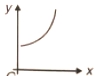
If slope of curve is first positive, then zero and after that became negative, so best represented of following graph which satisfied above condition
1. 
2. 
3. 
4. 

Find sin 5$°$
1. 0.087
2. 0.078
3. 0.056
4. 0.039

Find the value of sin 15$°$
1. $\frac{1}{2\sqrt{2}}$
2. $\frac{\sqrt{3}-1}{2\sqrt{2}}$
3. $\frac{2}{\sqrt{3}}$
4. $\frac{\sqrt{3}+1}{2\sqrt{2}}$

Find maximum and minimum value of y = 3sinx + 4cosx
1. 5 and -5
2. 3 and -3
4. 4 and -4
4. None of the above

Find the roots of equation $2{\mathrm{x}}^2-\mathrm{x}-3=0$
1. $x=\frac{3}{2} or x=-1$
2. $x=\frac{5}{2} or x=-2$
3. $x=2 or x=1$
4. $x=4 or x=2$