Please be patient as the PDF generation may take upto a minute.

The centre of mass of a body:
1.  Lies always at the geometrical centre
2.  Lies always inside the body
3.  Lies always outside the body
4.  Lies within or outside the body

A thin uniform wire is bent to form the two equal sides AB and AC triangle ABC, where AB=AC=5 cm. The third side BC, of length 6 cm, is made from uniform wire of twice the density of the first. The distance of centre of mass from A is:
1.  $\frac{34}{11} \mathrm{cm}$
2.  $\frac{11}{34} \mathrm{cm}$
3.  $\frac{34}{9} \mathrm{cm}$
4.  $\frac{11}{45} \mathrm{cm}$

A man of mass M stands at one end of a plank of length L which lies at rest on a frictionless surface. The man walks to other end of the plank. If the mass of the plank is $\frac{\mathrm{M}}{3}$, then the distance that the man moves relative to ground is:
1.  $\frac{3\mathrm{L}}{4}$
2.  $\frac{\mathrm{L}}{4}$
3.  $\frac{4\mathrm{L}}{5}$
4.  $\frac{\mathrm{L}}{3}$

Two particles bearing mass ratio n:1are interconnected by a light inextensible string that passes over a smooth pulley. If the system is released, then the of the centre of mass of the system is:
1.  ${\left(\mathrm{n}-1\right)}^2 \mathrm{g}$
2.  ${\left(\frac{\mathrm{n}+1}{\mathrm{n}-1}\right)}^2 \mathrm{g}$
3.  ${\left(\frac{\mathrm{n}-1}{\mathrm{n}+1}\right)}^2 \mathrm{g}$
4.  $\left(\frac{\mathrm{n}+1}{\mathrm{n}-1}\right)\mathrm{g}$

A particle of mass 3m is projected from the ground at some angle with horizontal. The horizontal range is R. At the height point of its path it breaks into two pieces m and 2m. The smaller mass comes to rest and larger mass finally falls at a distance x from the point of projection where x is equal to
1.  $\frac{3\mathrm{R}}{4}$
2.  $\frac{3\mathrm{R}}{2}$
3.  $\frac{5\mathrm{R}}{4}$
4.  $3\mathrm{R}$

A particle of mass 1 g moving with a velocity ${\overrightarrow{\mathrm{u}}}_1=\left(3\hat{\mathrm{i}}-2\hat{\mathrm{j}}\right){\mathrm{ms}}^{-1}$ experiences a perfectly inelastic collision with another particle of mass 2 g and velocity ${\overrightarrow{\mathrm{u}}}_2=\left(4\hat{\mathrm{j}}-6\hat{\mathrm{k}}\right){\mathrm{ms}}^{-1}$. The velocity of the combined particle is:
1.  $\hat{\mathrm{i}}+2\hat{\mathrm{j}}-4\hat{\mathrm{k}}$
2.  $\hat{\mathrm{i}}-2\hat{\mathrm{j}}+4\hat{\mathrm{k}}$
3.  $\hat{\mathrm{i}}-2\hat{\mathrm{j}}-4\hat{\mathrm{k}}$
4.  $\hat{\mathrm{i}}+3.33\hat{\mathrm{j}}+4\hat{\mathrm{k}}$

Moment of inertia of a disc about O O' is:
                        
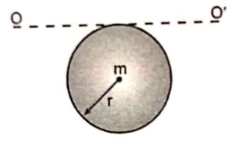
1.  $\frac{3 \mathrm{m} {\mathrm{r}}^2}{2}$
2.  $\frac{\mathrm{m} {\mathrm{r}}^2}{2}$
3.  $\frac{5 \mathrm{m} {\mathrm{r}}^2}{2}$
4.  $\frac{5 \mathrm{m} {\mathrm{r}}^2}{4}$

Three rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is:
                                         
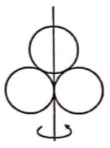
1.  $\sqrt{\frac{5}{3}}\mathrm{r}$
2.  $\sqrt{\frac{5}{6}}\mathrm{r}$
3.  $\sqrt{\frac{7}{3}}\mathrm{r}$
4.  $\sqrt{\frac{7}{6}}\mathrm{r}$

Three bodies have equal masses m. Body A is solid cylinder of radius R, body B is a square lamina of side R, and body C is a solid sphere of radius R. Which body has the smallest moment of inertia about an axis passing its centre of mass and perpendicular to the plane (in case of lamina)
1.  A
2.  B
3.  C
4.  A and C both

Find the moment of inertia of a plate cut in shape of a right angled triangle of mass M, side AC=BC=a about an axis perpendicular to the plane of the plate and passing through the mid point of side AB
                           
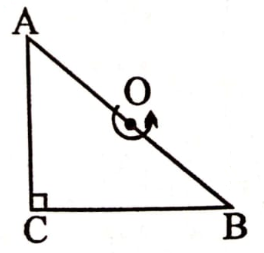
1.  $\frac{{\mathrm{Ma}}^2}{12}$
2.  $\frac{{\mathrm{Ma}}^2}{6}$
3.  $\frac{{\mathrm{Ma}}^2}{3}$
4.  $\frac{2{\mathrm{Ma}}^2}{3}$

A uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings ${\mathrm{T}}_1/{\mathrm{T}}_2$ is:
                                 
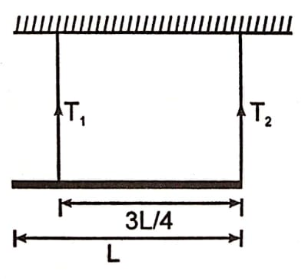
1.  1:1
2.  1:2
3.  2:1
4.  4:3

A uniform rod of length l is placed symmetrically on two walls as shown in figure. The rod is in equilibrium. If ${\mathrm{N}}_1$ and ${\mathrm{N}}_2$ are the normal forces exerted by the walls on the rod then
                               
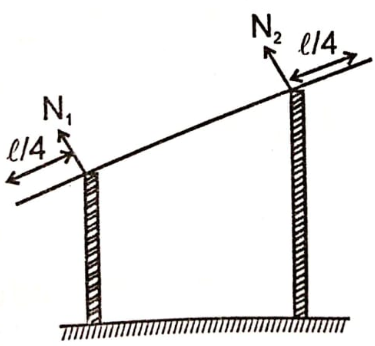
1.  ${\mathrm{N}}_1 > {\mathrm{N}}_2$
2.  ${\mathrm{N}}_1 < {\mathrm{N}}_2$
3.  ${\mathrm{N}}_1 = {\mathrm{N}}_2$
4.  ${\mathrm{N}}_1$ and ${\mathrm{N}}_2$ would be in the vertical directions.

A weightless rod is acted on by upward parallel forces of 2N and 4N at the ends A and B respectively. The total length of the rod AB=3m. To keep the rod in equilibrium a force of 6N should act in the following manner:
1.  Downwards at any point between A and B.
2.  Downwards at mid point of AB.
3.  Downwards at a point C such that AC=1 m.
4.  Downwards at a point D such that BD=1 m.

A thin hoop of weight 500 N and radius 1 m rests on a rough inclined plane as shown in the figure. The minimum coefficient of friction needed for this configuration is
                                
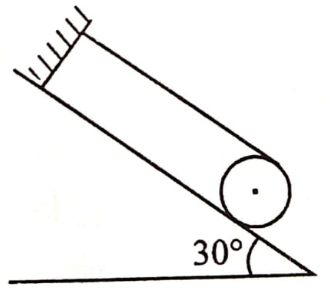
1.  $\frac{1}{3\sqrt{3}}$
2.  $\frac{1}{\sqrt{3}}$
3.  $\frac{1}{2}$
4.  $\frac{1}{2\sqrt{3}}$

Same number of books are placed in four bookcases as shown. Which bookcase is most likely to topple forward if pulled a little at the top towards right:
1. 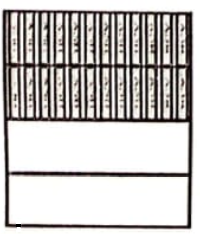   2.    3.    4.  

A uniform cube of side 'b' and mass M rest on a rough horizontal table. A horizontal force F is applied normal to one of the face at a point, at a height 3b/4 above the base. What should be the coefficient of friction ($\mathrm{\mu }$) between cube and table so that is will tip about an edge before it starts slipping?
                                
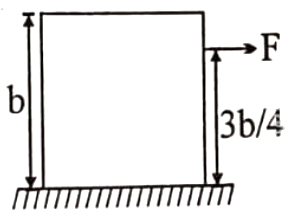
1.  $\mathrm{\mu }>\frac{2}{3}$
2.  $\mathrm{\mu }>\frac{1}{3}$
3.  $\mathrm{\mu }>\frac{3}{2}$
4.  $\frac{1}{2}$

A pulley is hinged at the centre and a massless thread is wrapped around it. The thread is pulled with a constant force F starting from rest. As the time increases,
                               
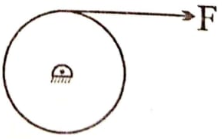
1.  its angular velocity increases, but force on hinge remains constant
2.  its angular velocity remains same, but force in hinge increases
3.  its angular velocity increases and force on hinge increases
4.  its angular velocity remains same and force on hinge is constant

A ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is:
                         
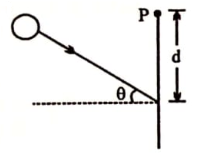
1.  2 mvd
2.  2 mvd cos$\mathrm{\theta }$
3.  2 mvd sin$\mathrm{\theta }$
4.  zero

Two uniform spheres of mass M have radii R and 2R. Each sphere is rotating about a fixed axis through a diameter. The rotational kinetic energies of the spheres are identical. What is the ratio of the magnitude of the angular momenta of these spheres? That is, $\frac{{\mathrm{L}}_{2\mathrm{R}}}{{\mathrm{L}}_{\mathrm{R}}}=$
1.  $4$
2.  $2\sqrt{2}$
3.  $2$
4.  $\sqrt{2}$

A child with mass m is standing at the edge of a disc with momentum of inertia I, radius R, and initial angular velocity $\mathrm{\omega }$. See figure given below. The child jumps off the edge of the disc with tangential velocity v with respect to the ground. The new angular velocity of the disc is
                                   
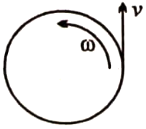
1.  $\sqrt{\frac{{\mathrm{I\omega }}^2-{\mathrm{mv}}^2}{\mathrm{I}}}$
2.  $\sqrt{\frac{\left(\mathrm{I}+{\mathrm{mR}}^2\right){\mathrm{\omega }}^2-{\mathrm{mv}}^2}{\mathrm{I}}}$
3.  $\frac{\mathrm{I\omega }-\mathrm{mvR}}{\mathrm{I}}$
4.  $\frac{\left(\mathrm{I}+{\mathrm{mR}}^2\right)\mathrm{\omega }-\mathrm{mvR}}{\mathrm{I}}$

A mass m is moving at speed v perpendicular to a rod of length d and mass M=6m which pivots around a frictionless axle running through its centre. It strikes and sticks to the end of the rod. The moment of inertia of the rod about its centre is ${\mathrm{Md}}^2/12$. Then the angular speed of the system right after the collision is
1.  2v/d
2.  2v/(3d)
3.  v/d
4.  3v/(2d)

A body kept on a smooth horizontal surface is pulled by a constant horizontal force applied at the top point of the body. If the body rolls purely on the surface, its shape can be:
1.  thin pipe
2.  uniform cylinder
3.  uniform sphere
4.  thin spherical shell

As shown in the figure, a disc of mass m is rolling without slipping an angular velocity $\mathrm{\omega }$. When it crosses point B disc will be in:
                     
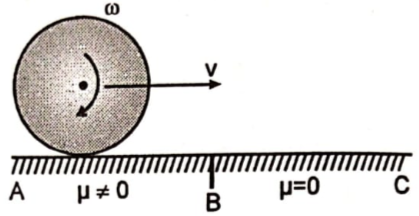
1.  translational motion only
2.  pure rolling motion
3.  rotational motion only
4.  none of these

A large spool of rope lies on the ground as shown in the fig. The end, labelled X is pulled a distance S in the horizontal direction. The spool rolls without slipping. The centre of mass of the spool moves a distance
               
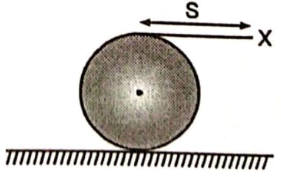
1.  2 S
2.  S
3.  S/2
4.  S/4

A plank of mass M is placed over smooth inclined plane and a sphere is also placed over the plank. Friction is sufficient between sphere and plank. If plank and sphere are released from rest, the frictional force on sphere is:
                                 
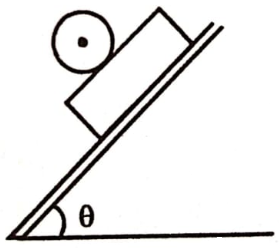
1.  up the plane
2.  down the plane
3.  horizontal
4.  zero