Ray Optics - NEET 2020 Contact Number: 9667591930 / 8527521718Ray Optics - NEET 2020 Contact Number: 9667591930 / 8527521718Two identical glass \(\left(\mu_g = \frac{3}{2}\right )\) equiconvex lenses of focal length \(f\) each are kept in contact. The space between the two lenses is filled with water \(\left(\mu_w = \frac{4}{3}\right)\). The focal length of the combination is:
| 1. | \(\dfrac{f}{3}\) | 2. | \(f\) |
| 3. | \(\dfrac{4f}{3}\) | 4. | \(\dfrac{3f}{4}\) |
An air bubble in a glass slab with a refractive index \(1.5\) (near-normal incidence) is \(5~\text{cm}\) deep when viewed from one surface and \(3~\text{cm}\) deep when viewed from the opposite surface. The thickness (in \(\text{cm}\)) of the slab is:
| 1. | \(8\) | 2. | \(10\) |
| 3. | \(12\) | 4. | \(16\) |
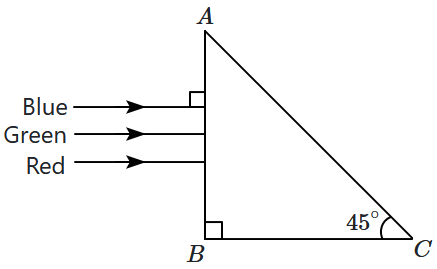
| 1. | separate the blue colour part from the red and green colour. |
| 2. | separate all three colours from one another. |
| 3. | not separate the three colours at all. |
| 4. | separate the red colour part from the green and blue colours. |
A ray of light is incident at an angle of incidence, \(i\), on one face of a prism of angle \(A\) (assumed to be small) and emerges normally from the opposite face. If the refractive index of the prism is \(\mu,\) the angle of incidence \(i\), is nearly equal to:
1. \(\mu A\)
2. \(\frac{\mu A}{2}\)
3. \(\frac{A}{\mu}\)
4. \(\frac{A}{2\mu}\)
| 1. | \(1.8 \times 10^8 ~\text{m/s}\) | 2. | \(2.4 \times 10^8~\text{m/s}\) |
| 3. | \(3.0 \times 10^8~\text{m/s}\) | 4. | \(1.2 \times 10^8~\text{m/s}\) |
A beam of light coming from a rarer medium is partially reflected from the surface of a denser medium and partially refracted into the denser medium. If the reflected and the refracted rays are perpendicular to each other and the ratio of the refractive indices of the denser and rarer medium is , the angle of refraction will be -
1.
2.
3.
4.
Two convex lens A and B, each of focal length 30 cm are separated by 30 cm, as shown in the figure. An object O is placed at a distance of 40 cm to the left of lens A.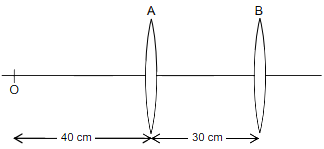
What is the distance of the final image formed by this lens system?
1. 120 cm to the right of lens A
2. 90 cm to the right of lens A
3. 22.5 cm to the right of lens B
4. 45 cm to the right of lens B
A person can see objects clearly only when they lie between \(50\) cm and \(400\) cm from his eyes. In order to increase the maximum distance of distinct vision to infinity, the type and power of the correcting lens, the person has to use, will be:
| 1. | convex, \(+2.25\) D | 2. | concave, \(-0.25\) D |
| 3. | concave, \(-0.2\) D | 4. | convex, \(+0.5\) D |
| 1. | \(46.0\text{cm}\) | 2. | \(50.0\text{cm}\) |
| 3. | \(54.0\text{cm}\) | 4. | \(37.3\text{cm}\) |
A concave mirror of the focal length \(f_1\) is placed at a distance of \(d\) from a convex lens of focal length \(f_2\). A beam of light coming from infinity and falling on this convex lens-concave mirror combination returns to infinity. The distance \(d\) must be equal to:
1. \(f_1+f_2\)
2. \(-f_1+f_2\)
3. \(2f_1+f_2\)
4. \(-2f_1+f_2\)
You are standing on the shore of a lake. You spot a fish swimming below the lake surface. You want to kill the fish first by throwing a spear and next, by pointing a high-power laser torch. How should you aim the spear and torch, respectively, from the options given below?
I. above the apparent position of the fish
II. below the apparent position of the fish
III. directly at the apparent position of the fish
1. SPEAR: II : LASER: III
2. SPEAR: I : LASER: II
3. SPEAR: II : LASER: II
4. SPEAR: III : LASER: III
A boy is trying to start a fire by focusing sunlight on a piece of paper using an equiconvex lens of a focal length of \(10\) cm. The diameter of the sun is \(1.39\times10^9\) m and its mean distance from the earth is \(1.5\times10^{11}\) m. What is the diameter of the sun's image on the paper?
| 1. | \(9.2\times10^{-4}\) m | 2. | \(6.5\times10^{-4}\) m |
| 3. | \(6.5\times10^{-5}\) m | 4. | \(12.4\times10^{-4}\) m |
| 1. | \(180^\circ-3A\) | 2. | \(180^\circ-2A\) |
| 3. | \(90^\circ-A\) | 4. | \(180^\circ+2A\) |
In an astronomical telescope in normal adjustment, a straight line of length \(L\) is drawn on the inside part of the objective lens. The eye-piece forms a real image of this line. The length of this image is \(l.\) The magnification of the telescope is:
1. \(\frac{L}{l}+1\)
2. \(\frac{L}{l}-1\)
3. \(\frac{L+1}{l-1}\)
4. \(\frac{L}{l}\)
There is an equiconvex glass lens with radius of each face as R and = 3/2 and
= 4/3. If there is water in object space and air in image space, then the focal length is
(1) 2R
(2) R
(3) 3R/2
(4) 3 R
The relation between , if the behavior of light rays is as shown in the figure:
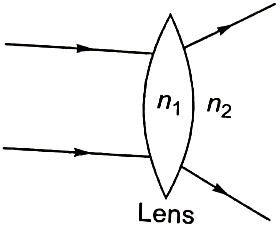
1.
2.
3.
4.
A person can see clearly only the objects situated in the range of 50 cm to 300 cm. He went to an optometrist who prescribed him a lens of a certain power to increase the maximum distance of his vision to infinity, i.e., it corrected the nearsightedness. However, upon using the prescribed lens the person discovered that the near point of his vision has shifted from 50 cm to a distance "d". What is the value of d?
1. 60 cm
2. 100 cm
3. 40 cm
4. 500 cm
A given ray of light suffers minimum deviation in an equilateral prism P. Additional prism Q and R of identical shape and of the same material as P is now added as shown in the figure. The ray will now suffer:
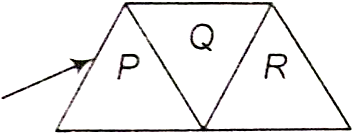
1. greater deviations
2. no deviation
3. same deviation as before
4. total internal reflection