Please be patient as the PDF generation may take upto a minute.

Given in the figure are two stationary blocks A and B of weight 20 N and 100 N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is
 

1. 100 N
2. 80 N
3. 120 N
4. 150 N

The figure shows the position - time (x - t) graph of one - dimensional motion of a body of mass 0.4 kg. The magnitude of each impulse is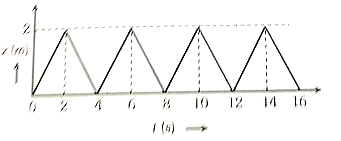 

1. 0.2 Ns
2. 0.4 Ns
3. 0.8 Ns
4. 1.6 Ns

A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block will be
$1. \mathrm{P}$
$2. \frac{\mathrm{Pm}}{\mathrm{M} + \mathrm{m}}$
$3. \frac{\mathrm{PM}}{\mathrm{M} + \mathrm{m}}$
$4. \frac{\mathrm{Pm}}{\mathrm{M} - \mathrm{m}}$

A solid sphere of mass 2 kg is resting inside a cube as shown in the figure. The cube is moving with a velocity $\mathrm{v} = (5\mathrm{t} \hat{\mathrm{i}} + 2\mathrm{t} \hat{j})$m/s. Here t is the time in second. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube. (Take g = 10 m/s${}^2$)
         
$1. \sqrt{29} \mathrm{N}$
$2. 29 \mathrm{N}$
$3. 26 \mathrm{N}$
$4. \sqrt{89} \mathrm{N}$
$$

Two wooden blocks are moving on a smooth horizontal surface such that the mass m remains stationary with respect to block of mass M as shown in the fig. The magnitude of force P is
     
1. (M + m) g tan $\mathrm{\beta }$
2. g tan $\mathrm{\beta }$
3. (M + m) g cosec $\mathrm{\beta }$
4. mg cos $\mathrm{\beta }$

A block A of mass 2 kg rests on another block B of mass 8 kg which rests on a  horizontal floor, as shown in the fig. The coefficient of coefficient of friction between A and B is 0.2 while that between B and the floor is 0.5. When a horizontal force of 30 N is applied on B, the force of friction between A and B is                                                                  (Take g = 10 m/s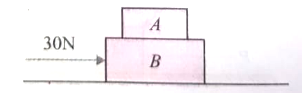${}^2$)

1. zero
2. 4 N
3. 5 N
4. 6 N

The elevator shown in fig. is descending with an acceleration of 2 m/s${}^2$. The mass of the block A is 0.5 kg. The force exerted by the block A and on block B is (Take g = 10 m/s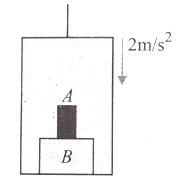${}^2$)

1. 2 N
2. 4 N
3. 6 N
4. 8 N

The kinetic energy K of a particle moving along a circle of radius R depends on the distance covered S as $\mathrm{K}={\mathrm{as}}^2$ where a is a constant. The force acting on the particle is 
1. $\frac{2as}{R}$
2. $2as{\left(1+\frac{S^2}{R^2}\right)}^{1/2}$
 
3. 2as
4. $\frac{2a{R}^2}{s}$

An iron chain of length L lies on a rough table. The coefficient of friction between the chain and the table is $\mathrm{\mu }$. What maximum fraction of the chain can hang from the edge of the table?
1. $\frac{\mu +1}{\mu }$
2. $\frac{1-\mu }{\mu }$
3. $\frac{\mu }{\mu +1}$
4. $\frac{\mu }{1-\mu }$

A body of mass m, rests on a horizontal floor with which it has a coefficient of static friction $\mathrm{\mu }$. It is desired to make the body move by applying the minimum possible force F is
1. $\mathrm{\mu } \mathrm{mg}$
2. $\frac{\sqrt{1+\mu }}{\mu }mg$
3. $\mu \sqrt{1+{\mu }^2}mg$
4. $\frac{\mu mg}{\sqrt{1+{\mu }^2}}$

A mass 2m lies on a fixed, smooth cylinder. An ideal string attached to 2m passes over the cylinder to mass m. Then the value of angle $\mathrm{\theta }$ for which system is in equilibrium is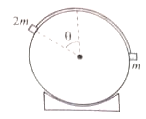 

1. 40$°$
2. 45$°$
3. 60$°$
4. 30$°$

A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is $\mu =\frac{1}{\sqrt{3}}$. The maximum height up to which the particle can remain stationary is 
1. $\frac{R}{2}$
2. $\left(1-\frac{\sqrt{3}}{2}\right)R$
3. $\frac{\sqrt{3}}{2}R$
4. $\frac{3R}{8}$ 

A piece of wire is bent in the shape of a parabola $\mathrm{y}={\mathrm{kx}}^2$ (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is 
1. $\frac{a}{gk}$
2. $\frac{a}{2gk}$
3. $\frac{2\mathrm{a}}{\mathrm{gk}}$
4. $\frac{a}{4gk}$ 

All surface shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be:
 
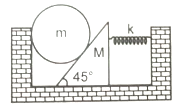
1. $\frac{2mg}{k}$
2. $\frac{\left(M+m\right)g}{\sqrt{2}k}$
3. $\frac{mg}{\sqrt{2}k}$
4. $\frac{mg}{k}$

Figure shows two blocks, each of mass m. The system is released form rest. If accelerations of blocks A and B at any instant (not initially) are ${\mathrm{a}}_1$ and ${\mathrm{a}}_2$, respectively, then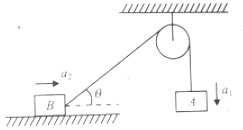

1. ${\mathrm{a}}_1={\mathrm{a}}_2\mathrm{cos\theta }$
2. ${\mathrm{a}}_2={\mathrm{a}}_1\mathrm{cos\theta }$
3. ${\mathrm{a}}_1={\mathrm{a}}_2$
4. None of these

Assuming that the block is always remains horizontal, hence the acceleration of B is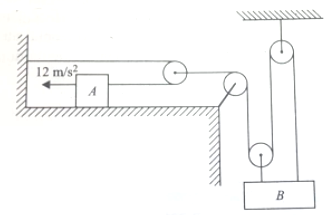 

1. 6 $\mathrm{m}/{\mathrm{s}}^2$
2. 2 $\mathrm{m}/{\mathrm{s}}^2$
3. 4 $\mathrm{m}/{\mathrm{s}}^2$
4. None of these

A given object takes n times more time to slide down 45$°$ rough inclined plane as it takes to slide down a perfectly smooth 45$°$ incline. The coefficient of kinetic friction between the object and the incline is 
1. $\sqrt{\frac{1}{1-n^2}}$
2. $\sqrt{1-\frac{1}{n^2}}$
3. $1-\frac{1}{n^2}$
4. $\frac{1}{2-n^2}$

Two blocks A(2 kg) and B (5 kg) rest one over the other on smooth horizontal plane. The coefficient of static and dynamic friction between A and B is the same and is equal to 0.80. The maximum horizontal force that can be applied to B in order that both A and B do not have relative motion is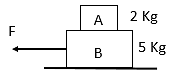 

1. 1.2 N
2. 42 N
3. 4.2 N
4. 56 N

A trolley A has a simple pendulum suspended from a fixed to its desk. A block B is in contact on its vertical side. The trolley is on horizontal rails and accelerates towards the right such that the block is just prevented from falling. The value of the coefficient of friction between A and B is 0.5. The inclination of the pendulum to the vertical is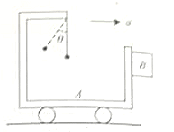

1. ${\tan }^{-1}\left(\frac{1}{2}\right)$
2. ${\tan }^{-1}\left(3\right)$
3. ${\tan }^{-1}\left(\sqrt{2}\right)$
4. ${\tan }^{-1}\left(2\right)$

Three blocks \(A\), \(B\) and \(C\) of mass \(3M\), \(2M\) and \(M\) respectively are suspended vertically with the help of springs \({PQ}\) and \({TU}\) and a string \({RS}\) as shown in Figure. The acceleration of blocks \(A\), \(B\) and \(C\) are \(a_{1} , a_{2}~ \text{and}~ a_{3}\) respectively.
                         
The value of acceleration \(a_{1}\) at the moment string \({RS}\) is cut will be: 
1. \(g\) downward
2. \(g\) upward
3. more than \(g\) downward
4. zero