Please be patient as the PDF generation may take upto a minute.

Drops of water fall from the roof of a building 20 m high at regular intervals
of time. The first drop reaching the ground at the same instant fifth drop
starts its fall. What are the distance  of second and third drops from roof? (g =
10 $m/s^2$)
1. 5.0 m and 1.25 m
2. 5.0 m and 2.25 m
3. 11.25 m and 5.0 m
4. 11.25 and 1.25 m

A particle is dropped vertically from rest from a height. The time taken by it to
fall through successive distances of 1 m will the be

A car drives along straight level frictionless road by an engine delivering constant power. Then velocity is directly proportional to
1. t 
2.$\frac{1}{\sqrt{t}}$
3.$\sqrt{t}$
4. None of these

A ball rolls off the top of stairway with a horizontal velocity of magnitude 1.8 m/s. The steps are 0.20 m high and 0.20 m wide. Which step will the ball hit first ?
1. First
2. Second
3. Third
4. Fourth

A car accelerates from rest at a constant rate $\alpha$ for some time after which it decelerates at a constant rate $\beta$ to come to rest. If the total time elapsed is t, the distance travelled by the car is:
1. $\frac{1}{2}\left(\frac{\alpha \beta }{\alpha +\beta }\right)t^2$
2. $\frac{1}{2}\left(\frac{\alpha +\beta }{\alpha \beta }\right)t^2$
3. $\frac{1}{2}\left(\frac{{\alpha }^2+{\beta }^2}{\alpha \beta }\right)t^2$
4. $\frac{1}{2}\left(\frac{{\alpha }^2-{\beta }^2}{\alpha \beta }\right)t^2$

A train accelerates from rest at a constant rate $\mathrm{}$\(\alpha\) for distance ${\mathrm{}}_{}$\(x_1\) and time \(t_1.\) After that, It retards to rest at a constant rate \(\beta\) $\mathrm{}$ for distance ${\mathrm{}}_{}$\(x_2\) and time ${\mathrm{}}_{}$\(t_2.\) Then it is found that:
1. \(\frac{x_{1}}{x_{2}}   =   \frac{\alpha}{\beta}   =   \frac{t_{1}}{t_{2}}\)
2. \(\frac{x_{1}}{x_{2}}   =   \frac{\beta}{\alpha}   =   \frac{t_{1}}{t_{2}}\)
3. \(\frac{x_{1}}{x_{2}}   =   \frac{\beta}{\alpha}   =   \frac{t_{2}}{t_{1}}\)
4. \(\frac{x_{1}}{x_{2}}   =   \frac{\alpha}{\beta}   =   \frac{t_{2}}{t_{1}}\)$\frac{{\mathrm{}}_{}}{}$

A smooth square platform ABCD is moving towards right with a uniform speed u. At what angle $\theta$ must a particle be projected from A with speed $v$ so that it strikes the point D ?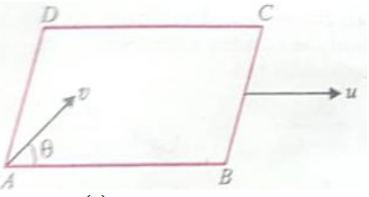

1. ${\sin }^{-1}$ $\left(\frac{u}{v}\right)$
2. ${\cos }^{-1}$ $\left(\frac{v}{u}\right)$
3. ${\sin }^{-1}$ $\left(\frac{v}{u}\right)$
4. ${\cos }^{-1}$ $\left(\frac{u}{v}\right)$

Time taken by the projectile to reach from A to B is t, then the distance AB is equal to: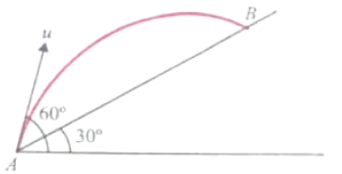

1. 2$ut$
2. $\sqrt{3} ut$
3. $\frac{\sqrt{3}}{2}ut$
4. $\frac{ut}{\sqrt{3}}$

A man in a lift ascending with an acceleration throws a ball vertically upwards with a velocity u and catches it after time ${\mathrm{t}}_1$. Afterwards, when the lift is descending with the same acceleration, the man again throws the ball vertically upwards and catches it after time ${\mathrm{t}}_2$. The velocity of the projection of the ball:
$1. \frac{{\mathrm{gt}}_1{\mathrm{t}}_2}{\left({\mathrm{t}}_1-{\mathrm{t}}_2\right)}$
$2. \frac{{\mathrm{gt}}_1{\mathrm{t}}_2}{\left({\mathrm{t}}_1+{\mathrm{t}}_2\right)}$
$3. \frac{{\mathrm{gt}}_1{\mathrm{t}}_2}{2\left({\mathrm{t}}_1-{\mathrm{t}}_2\right)}$
$4. \frac{{\mathrm{gt}}_1{\mathrm{t}}_2}{2\left({\mathrm{t}}_1+{\mathrm{t}}_2\right)}$

Two particles are separated by a horizontal distance R on the ground. Those are projected simultaneously with velocities u and u/$\sqrt{3}$ at angles of projection ${60}^0$ and 150° with the horizontal direction so that they approach each other in the same plane. The time after which they meet at point on the horizontal plane is:
1. u/2 R
2. 2 R/u
3. u/R
4. R/u

A vertical circular disc has different grooves along various chords as shown in fig. The particles are released from upper end O. The times taken by the particles to reach the ends of the grooves OA, OB and OC respectively are in the ratio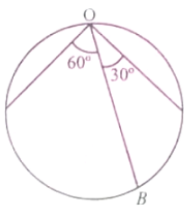

1. 1:1:1
2. 1:2:$\sqrt{3}$
3. 1: $\sqrt{3}$:2
4. 1: $\sqrt{3}$: $\sqrt{2}$

A boy throws a ball upwards with velocity $v_0$. The wind imparts a horizontal acceleration of 4 $m/s^2$ to the left. The angle $\theta$ at which the ball must be thrown so that the ball returns to the boy’s hand is (g = 10 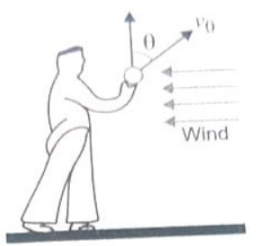$m/s^2$)

1. ${\tan }^{-1}$ (1.2)
2. ${\tan }^{-1}$ (O.2)
3. ${\tan }^{-1}$ (2)
4. ${\tan }^{-1}$ (O.4)

Two inclined planes OA and OB intersect is a horizontal plane having their inclinations $\alpha$ and ß with the horizontal as shown in fig. A particle is projected from point P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q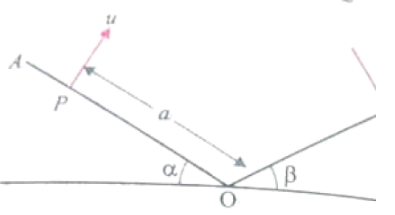 

If $\alpha$ = ${30}^0$ $\beta$ = ${30}^0$, the time of flight from P to Q is
1. u/g
2. $\sqrt{3}$u/g
3. $\sqrt{2}$u/g
4. 2 u/g

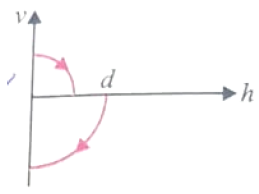
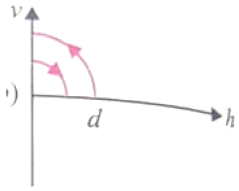
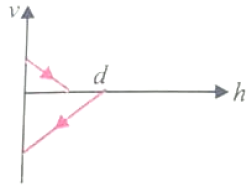
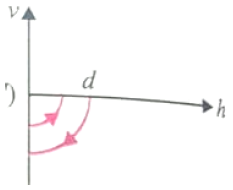
A ball is dropped vertically from a height above the ground. It hits the ground and bounced up vertically to a height d/2. neglecting subsequent motion and the air resistance, its velocity v with height h above the ground can be represented as 
1.
2.
3.
4.

A point P moves in counter-clockwise direction on a circular path as shown in fig. The movement of ‘P’ is such that it sweeps out a length s = $t^3$+5, where s is in metres and t is in seconds. The radius of the path is 20 m. The acceleration of
‘P’ when t = 2 s is nearly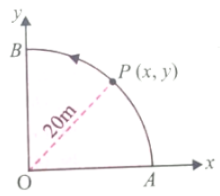

1. 13 $m/s^2$
2. 12 $m/s^2$
3. 7.2 $m/s^2$
4. 14 $m/s^2$

A particle is moving with velocity $\overrightarrow{v}$ = $K\left(y\hat{i}+x\hat{j} \right)$, where K is a constant. The
general equation for its path is 
1. y =$x^2$ + constant
2. y²=x + constant
3. xy= constant
4. y²= $x^2$+ constant