A particle executes SHM of type x = a sin t. It takes time , from x = 0 to to x = a. The ratio will be
1. 1 : 1
2. 1 : 2
3. 1 : 3
4. 2 : 1
Displacement-time equation of particle SHM is, x = 4 sin . Here, x is in centimeters and t in seconds. The amplitude of oscillation of the particle is approximately
1. 5 cm
2. 6 cm
3. 7 cm
4. 9 cm
A spring has force constant K and a mass m is suspended from it. The spring is cut in two parts in the ratio 1:3, and the same mass is suspended from the larger part. If the frequency of oscillation in the first case in n, then the frequency in the second case will be:
1. 2n
2. 3n
3.
3.
Two light springs of force constants (each 3.2 N/m) and a block of mass 'm' ( = 200 g) are in one line AB on a smooth horizontal table such that one end of each spring is fixed on a rigid support and the other end is free as shown in fig. The distance CD between the free ends of spring is 60.0 cm. If block moves along with AB with a velocity 120 cm/s in between the springs, the period of oscillations of the block is
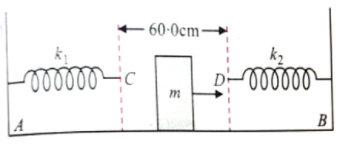
(1) 1.0 s
(2) 1.57 s
(3) 2.57 s
(4) 3.57 s
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm support. If each spring has to force constant k, the period of oscillation of the body (assuming the springs as massless) is: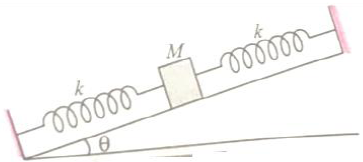
1.
2.
3.
4.
A particle of mass m is attached to three springs A, B and C of equal force constant k. If the particle is pushed a little towards any one of the springs and left, find the time period of its oscillations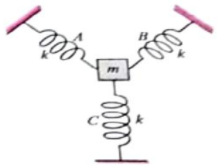
1.
2.
3.
4.
A simple pendulum has a length l. The inertial and gravitational masses of the bob are and respectively. Then the time period is given by:
1.
2.
3.
4.
A and B are fixed points and the mass M is tied by strings at A and B. If the mass M is displaced slightly out of this plane and released, it will execute oscillations with a period ( Given AM = BM = L, AB = 2d)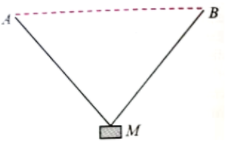
1.
2.
3.
4.
The velocity of a particle at an instant in simple harmonic oscillation is given by , where x is in the metre. The maximum velocity of that particle is:
(1) 6 m/s
(2) 9 m/s
(3) 12 m/s
(4) 16 m/s
A cubical body of side L, relative density just floats in water. It is pressed and then released so that it oscillates vertically. Then its frequency of oscillation is:
1.
2.
3.
4.
A pendulum has period T for small oscillations. An obstacle is placed directly beneath the pivot so that only the lowest one-quarter of the string can follow the pendulum bob when it swings towards the left of its resting position as shown in fig. The pendulum is released from rest at a certain point A. The time taken by it to return to that point is :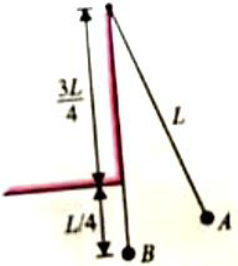
1. T/4
2. T/2
3. T
4. 3T/4
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in fig. The time period of small oscillations is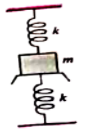
1.
2.
3. +
4. +
Two simple pendulums of lengths 60 cm and 64 cm are respectively hanging vertically one in front of the other. If they are set in motion simultaneously, the time taken for one to gain complete oscillation on the other is:
1. 29.3 s
2. 39.3 s
3. 49.3 s
4. 59.3 s
A uniform rod of length L and mass M is pivoted at the center. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle o in one direction and released. The frequency of oscillating is
1.
2.
3.
4.
One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to a massless spring of spring constant k. A mass m hangs freely from the free end of the string. The area of cross-section and Young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to
1.
2.
3.
4.
A highly rigid cubical block A of small mass Mand side L is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity n such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force Fis applied perpendicular to one of the side faces of A. After the force is withdrawn, block A executes small oscillations, the time period of which is given by
1.
2.
3.
4.
Two particles P and Q are executing S.H.M, across the same straight line whose equation is given as and . An observer, at t = 0, observes the particle P at a distance A/ to the right of mean position O and moving towards the right, while Q at A/2 to the left of mean position 0 and moving towards left as shown. Then () is equal to 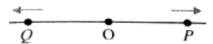
(a) /12
(b) 7/12
(c) 5/12
(d) 13/12
A system is shown in fig consists of the massless pulley, a spring of force constant k and block of mass m. If block is just slightly displaced vertically down from its equilibrium position and released, the period of vertical oscillations is 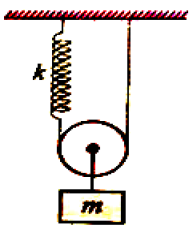
1.
2.
3.
4.
In the arrangement in fig., a solid sphere is attached to spring and displaced. It starts executing SHM without slipping. The time period of the sphere is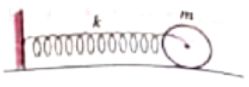
1.
2.
3.
4.
A cylindrical piston of mass M and area of cross-section A slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of gas at pressure P. The cylinder is kept with its axis horizontal. If the piston is disturbed from its equilibrium position, it oscillates simple harmonically. Assuming that the temperature remains constant, the period, the period of oscillation will be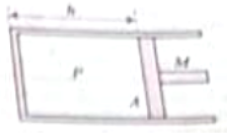
1.
2.
3.
4.